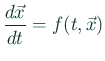Next: 4.1.0.2 注意 2 Up: 4.1 問題の説明 Previous: 4.1 問題の説明
後で数学的な説明をするときのために、問題をベクトル、行列を用いて書き 換えましょう。
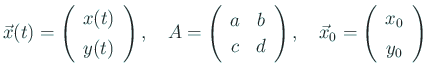
| (1) | 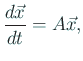 |
| (2) |
初期値問題 (1), (2) の解は平面内での点の運動を表わしていると考えるこ
とが出来ます。初期値 ![]() を色々と変えて、それに対応する解
を色々と変えて、それに対応する解 ![]() の軌跡(解軌道と呼びます)を描いてみましょう。この解軌道を考える時
の空間(ここでは平面
の軌跡(解軌道と呼びます)を描いてみましょう。この解軌道を考える時
の空間(ここでは平面
![]() )を相空間(phase space)16と呼びます。
)を相空間(phase space)16と呼びます。
![]() とおくと、方程式 (1) は
とおくと、方程式 (1) は