Next: 3.3.0.1 問題5-3 Up: 3 常微分方程式の初期値問題の数値解法 Previous: 3.2.5.1 例題 5.2
3.2.5 で解説した Euler 法は簡単で、
これですべてが片付けば喜ばしいのですが、
残念ながらあまり効率が良くありません。高精度の解を計算するために
は、分割数 ![]() をかなり大きく取る(=大量の計算をする)必要があります。特
別な場合13を除けば、実際に使われることは滅多にないでしょう。率直
にいって実用性は低いです。
をかなり大きく取る(=大量の計算をする)必要があります。特
別な場合13を除けば、実際に使われることは滅多にないでしょう。率直
にいって実用性は低いです。
より高精度の公式は、現在まで様々なものが開発されていますが、比較的簡
単で、精度がまあまあ高いものに Runge-Kutta 法と呼ばれるものがあります。
それは ![]() から
から ![]() を求める漸化式として次のものを用います。
を求める漸化式として次のものを用います。
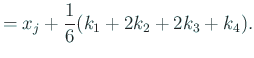 |
| reidai5-3.c |
/*
* reidai5-3.c --- 常微分方程式の初期値問題を Runge-Ketta 法で解く
* http://nalab.mind.meiji.ac.jp/~mk/program/ode_prog/reidai5-3.c
*/
#include <stdio.h>
#include <math.h>
int main(void)
{
/* 開始時刻と終了時刻 */
double a = 0.0, b = 1.0;
/* 初期値 */
double x0;
/* 変数と関数の宣言 */
int N,j;
double t,x,h,f(double,double),k1,k2,k3,k4;
/* 初期値の設定 */
x0 = 1.0;
/* 区間の分割数 N を入力してもらう */
printf("N="); scanf("%d", &N);
/* 小区間の幅 */
h = (b-a) / N;
/* 開始時刻と初期値のセット */
t = a;
x = x0;
printf("%f %f\n", t, x);
/* Runge-Kutta 法による計算 */
for (j = 0; j < N; j++) {
k1 = h * f(t, x);
k2 = h * f(t + h / 2, x + k1 / 2);
k3 = h * f(t + h / 2, x + k2 / 2);
k4 = h * f(t + h, x + k3);
x += (k1 + 2 * k2 + 2 * k3 + k4) / 6;
t += h;
printf("%f %f\n", t, x);
}
printf("%f %17.15f\n", t, x);
return 0;
}
/* 微分方程式 x'=f(t,x) の右辺の関数 f の定義 */
double f(double t, double x)
{
return x;
}
|
コンパイル・実行の結果は次のようになるはずです。
oyabun% gcc reidai5-3.c oyabun% ./a.out N=10 0.000000 1.000000 0.100000 1.105171 0.200000 1.221403 0.300000 1.349858 0.400000 1.491824 0.500000 1.648721 0.600000 1.822118 0.700000 2.013752 0.800000 2.225540 0.900000 2.459601 1.000000 2.718280 1.000000 2.718279744135166 ← たくさんの桁数を表示 oyabun% |
たった ![]() 等分なのに相対誤差が
等分なのに相対誤差が ![]() 以下になっています
(
以下になっています
(![]()
![]() であるので、相対誤差
=
であるので、相対誤差
=
![]() )。
Runge-Kutta 法の公式は Euler 法よりは大部面倒ですが、
それに見合うだけの価値があることが納得できるでしょう。
)。
Runge-Kutta 法の公式は Euler 法よりは大部面倒ですが、
それに見合うだけの価値があることが納得できるでしょう。