Next: 3.6 解析例 Up: 3 Mathematica でサウンドを扱う Previous: 3.4 Import[] によるサウンド・ファイルの読み込み
(考えてみたら、周期を一般の ![]() とした式を書くべきだな…)
とした式を書くべきだな…)
Mathematica には、 離散フーリエ変換をするための Fourier[ ] がある。
周期 ![]() の周期関数
の周期関数
![]() があるとき、
区間
があるとき、
区間 ![]() の
の ![]() 等分点
等分点
| (1) | 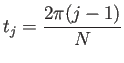 |
| (2) |
| (3) | 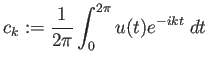 |
| (4) | 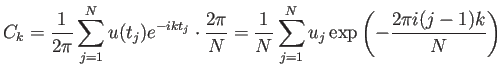 |
InverseFourier[] という逆変換が用意されている。
| 簡単に証明できる良く知られた事実 | ||||||||||||
|
Mathematica では、
長さ ![]() のリスト u={
のリスト u={
![]() } があるとき、
} があるとき、
|
v=Fourier[u,FourierParameters->{ |
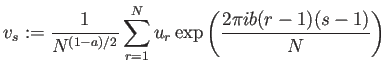
特に
v=Fourier[u,FourierParameters->{-1,-1}]
|
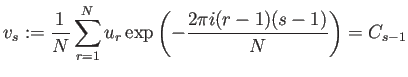
| 三角級数の係数を再生 |
a0 = 1
a = {1, 2, 3, 4, 5}
b = {6, 7, 8, 9, 10}
u[t_]:=a0/2+a . Table[Cos[n t],{n,Length[a]}]+b . Table[Sin[n t],{n,Length[b]}]
n = 12
ts = Table[2 Pi (j - 1)/n, {j, n}];
us = u[ts];
cs = Fourier[us, FourierParameters -> {-1, -1}]
A0 = 2 cs[[1]]
A = Table[cs[[k + 1]] + cs[[n - k + 1]], {k, 5}]
B = I Table[cs[[k + 1]] - cs[[n - k + 1]], {k, 5}]
|
桂田 祐史