H..5 等角写像 (写像関数) を可視化する (等高線を描く機能の応用)

複素平面内の任意の単連結領域$\Omega$ ($\ne\C$ ) に対して、 $\Omega$ から単位円盤 $D=\left\{z\in\C; \vert z\vert<1\right\}$ の上への等角写像 $f\colon\Omega\to D$ が存在する。それを $\Omega$ の写像関数と呼ぶ。

適当な追加条件を課すと写像関数は一意には定まる。例えば $z_0\in\Omega$ を任意に一つ選ぶと、

$$f(z_0)=0,\quad f'(z_0)>0$$

を満たす写像関数 $f$ は一意的に存在することが知られている。

$\Omega=D$ のとき、関数論で学ぶように

$$f(z)=\frac{z-z_0}{1-\overline{z_0}z}.$$

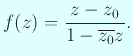
これを可視化してみよう。

一般に写像 $f\colon\Omega\to D$ を可視化するために、 $\Omega$ か $D$ の中に何かを描いて、 もう一方にはそれを写像したものを描く、という方法がある。 今の場合、$D$ は単位円盤であるから、 原点中心の同心円群 $\{w\in\C; \vert w\vert=r_i\}$ と、 原点を通る放射線群 $\{w\in\C; \arg w=\theta_j\}$ を 採用することが考えられる。 ただし $\{r_i\}$ , $\{\theta_j\}$ は $[0,1]$ , $[-\pi,\pi]$ の分割点である:

$$0=r_0<r_1<\cdots<r_m=1,\quad -\pi=\theta_0<\theta_1<\cdots<\theta_n=\pi.$$

$w=f(z)$ の実部と虚部の等高線を描く

[x,y]=meshgrid(-2:0.01:2,-2:0.01:2);
z=x+1i*y;

z0=0.5;
w=(z-z0)./(1-conj(z0)*z);

clf
hold on
m=20;
n=10;
levelangle=linspace(-pi,pi,m+1);
levelabs=linspace(0,1,n+1);

contour(x,y,angle(w),levelangle)
contour(x,y,abs(w),levelabs)
axis square

図: $w=f(z)=\dfrac{z-z_0}{1-\overline{z_0}z}$ , $z_0=1/2$ (はみ出る)

これで一応、写像の ``状況'' は分かるわけだが、 $\Omega$ からはみ出ているのが嫌味である。

うまい解決策が分からないので、次のようにして逃げている。 指定した点が指定した多角形の内部に含まれているかどうかを判定する in=inpolygon(x,y,xv,yv) という関数を利用する。

はみ出ないように

% メッシュを準備
[x,y]=meshgrid(-1.2:0.01:1.2,-1.2:0.01:1.2);
z=x+1i*y;

% 写像関数
z0=0.5;
w=(z-z0)./(1-conj(z0)*z);

% 等高線のレベル
m=20;
n=10;
levelangle=linspace(-pi,pi,m+1);
levelabs=linspace(0,1,n+1);

% 領域の内部にあるかどうか判定
t=linspace(0,1,100+1);
bx=cos(2*pi*t);
by=sin(2*pi*t);
indisk=inpolygon(x,y,bx,by);
outdisk=(1-indisk)*10;

clf;
subplot(1,2,1)
hold on
contour(x,y,angle(w)+outdisk,levelangle);
contour(x,y,abs(w)+outdisk,levelabs)
axis square

subplot(1,2,2)
hold on
contour(x,y,angle(z)+outdisk,levelangle);
contour(x,y,abs(z)+outdisk,levelabs)
axis square

図: $w=f(z)=\dfrac{z-z_0}{1-\overline{z_0}z}$ , $z_0=1/2$ (はみ出ない)