Next: е•ҸйЎҢ Up: гҒ®еҲқжңҹеҖӨе•ҸйЎҢгҒ® Green й–ўж•° Previous: 2.3 и§ЈгҒ®е…¬ејҸ
(гҒ“гӮҢгҒҜеҸӨгҒ„гғҶгӮӯгӮ№гғҲгҒ«ијүгҒӣгҒҰгҒ„гҒҹгӮӮгҒ®гҒ§гҒӮгӮӢгҖӮ)
дёҖиҲ¬гҒ® ![]() гҒ«еҜҫгҒ—гҒҰгҖҒйқһеҗҢж¬Ўж–№зЁӢејҸ
гҒ«еҜҫгҒ—гҒҰгҖҒйқһеҗҢж¬Ўж–№зЁӢејҸ
![\begin{jtheorem}% latex2html id marker 234
[Green й–ўж•°гҒ«гӮҲгӮӢзү№и§Ј]
$2$\ ж...
...°дҝӮж•°2йҡҺйқһеҗҢж¬Ўз·ҡеһӢODEгҒҫгҒҹгҒҫгҒҹ}) гҒ®зү№и§ЈгҒ§гҒӮгӮӢгҖӮ
\end{jtheorem}](img51.png)
|
гҒ“гҒ®е®ҡзҗҶгҒ«зҸҫгӮҢгҒҹй–ўж•° ![]() гҒ®гҒ“гҒЁгӮ’
еҫ®еҲҶж–№зЁӢејҸ (7) гҒ®
еҲқжңҹеҖӨе•ҸйЎҢгҒ® Green й–ўж•°гҒЁгӮҲгҒ¶гҖӮ
гҒ®гҒ“гҒЁгӮ’
еҫ®еҲҶж–№зЁӢејҸ (7) гҒ®
еҲқжңҹеҖӨе•ҸйЎҢгҒ® Green й–ўж•°гҒЁгӮҲгҒ¶гҖӮ
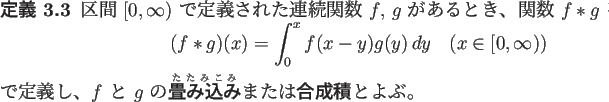
|
з•ігҒҝиҫјгҒҝгӮ’з”ЁгҒ„гӮӢгҒЁгҖҒ
дёҠгҒ® (9) гҒ® ![]() гҒҜ
гҒҜ ![]() гҒЁжӣёгҒ‘гӮӢгҒ“гҒЁгҒҢеҲҶгҒӢгӮӢгҖӮ
з•ігҒҝиҫјгҒҝгҒҜдёҠгҒ®е®ҡзҗҶгҒ®иЁјжҳҺгҒ«гӮӮжҙ»иәҚгҒҷгӮӢгҖӮ
гҒқгҒ®гҒҹгӮҒгҒ«е°‘гҒ—жә–еӮҷгҒ—гӮҲгҒҶгҖӮ
гҒЁжӣёгҒ‘гӮӢгҒ“гҒЁгҒҢеҲҶгҒӢгӮӢгҖӮ
з•ігҒҝиҫјгҒҝгҒҜдёҠгҒ®е®ҡзҗҶгҒ®иЁјжҳҺгҒ«гӮӮжҙ»иәҚгҒҷгӮӢгҖӮ
гҒқгҒ®гҒҹгӮҒгҒ«е°‘гҒ—жә–еӮҷгҒ—гӮҲгҒҶгҖӮ
![\begin{jproposition}[з•ігҒҝиҫјгҒҝгҒ®жҖ§иіӘ]
\begin{enumerate}[(1)]
\item $(c_1 ...
... гҒӘгӮүгҒ° $f\equiv 0$\ гҒҫгҒҹгҒҜ $g\equiv 0$.
\end{enumerate}\end{jproposition}](img58.png)
|
е®ҡзҗҶгҒ®иЁјжҳҺгҒ«е…ҘгӮӢеүҚгҒ«гҖҒ
е®ҡж•°дҝӮж•°![]() йҡҺз·ҡеһӢеҫ®еҲҶж–№зЁӢејҸгҒ®еҲқжңҹеҖӨе•ҸйЎҢ
йҡҺз·ҡеһӢеҫ®еҲҶж–№зЁӢејҸгҒ®еҲқжңҹеҖӨе•ҸйЎҢ
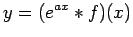
е®ҡзҗҶ
![]() ,
,
![]() гҒЁгҒҠгҒҸгҖӮ
гҒЁгҒҠгҒҸгҖӮ
![]() гҒҢ
гҒҢ
![]() гҒ®е ҙеҗҲгҒҜ
гҒ®е ҙеҗҲгҒҜ
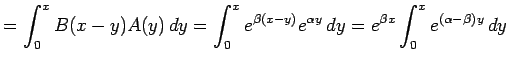 | ||
![$\displaystyle =e^{\beta x} \left[\frac{e^{(\alpha-\beta) y}}{\alpha-\beta}\right]_0^x = \dfrac{e^{\alpha x}-e^{\beta x}}{\alpha-\beta}.$](img77.png) |
 |