

Next: 3 二分法
Up: 2 標準固有値問題への帰着
Previous: 2.3 が正定値である場合にその Cholesky 分解を用いる方法
LAPACK で採用されている方法である。
残念ながら適当な参考文献が入手できていない。
LAPACK のドライバー・ルーチン spbstf の
ソース・プログラム dpbstf.f 中の
注釈くらいしか参考になるものがない。
なお、LAPACK のソースをサーチするには
が便利である。
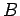 を
を
の形に分解するのだが、
通常の Cholesky 分解とは異なり、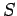 は上三角行列ではなく、
は上三角行列ではなく、
のような行列である。ここで 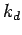 は半バンド幅である。
は半バンド幅である。
とおくと、
前小節の補題 2.4 に
より 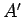 は対称であることが分かる。
は対称であることが分かる。
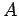 ,
, 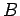 が帯行列である場合、
が帯行列である場合、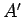 も (やや帯幅は増えるものの) 帯行列に
なる。
も (やや帯幅は増えるものの) 帯行列に
なる。


Next: 3 二分法
Up: 2 標準固有値問題への帰着
Previous: 2.3 が正定値である場合にその Cholesky 分解を用いる方法
桂田 祐史
2014-05-27
![]() を
を
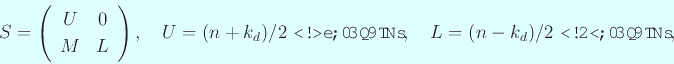
![]() ,
, ![]() が帯行列である場合、
が帯行列である場合、![]() も (やや帯幅は増えるものの) 帯行列に
なる。
も (やや帯幅は増えるものの) 帯行列に
なる。