

Next: 2.4 split Cholesky 分解を用いる方法
Up: 2 標準固有値問題への帰着
Previous: 2.2 が正則な場合に使える、ある素朴な方法
(この項の要点は式番号をふった式にある。)
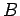 が正定値 (実対称で固有値がすべて正) である場合、Cholesky 分解
が正定値 (実対称で固有値がすべて正) である場合、Cholesky 分解
|
(2) |
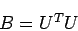 |
を代入して (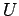 は正則な上三角行列であり、
特に対角成分が正であるものを選ぶことができ、その場合は一意的に決定される)
は正則な上三角行列であり、
特に対角成分が正であるものを選ぶことができ、その場合は一意的に決定される)
両辺に
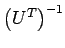 をかけると
をかけると
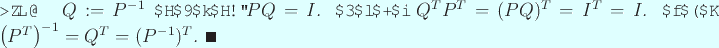
なお、
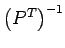 のことをしばしば
のことをしばしば 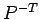 と書く人が多い
(個人的には悪趣味だと感じているが)。
と書く人が多い
(個人的には悪趣味だと感じているが)。
そこで
|
(3) |
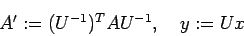 |
とおくと明らかに
|
(4) |
|
|
 |
|
(5) |
|
|
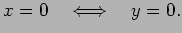 |
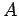 が実対称であれば、
が実対称であれば、
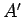 も実対称である。
これは次の補題から分かる。
も実対称である。
これは次の補題から分かる。
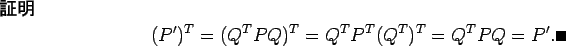
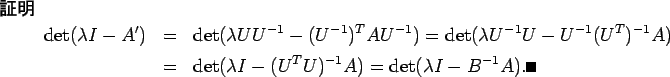
ここまでをまとめておこう。
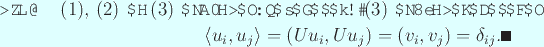
さて、実対称行列 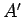 の標準固有値問題については、
Rayleigh 商
の標準固有値問題については、
Rayleigh 商
が重要な役目を果たすが、
これについては次の補題が成り立つ。
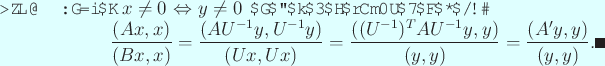
![\begin{jremark}[数値計算する上での注意]
ただし、
$A$, $B$ が�...
...��夫が有用である。
後述の Lanczos 法の節を見よ。
\end{jremark}](img53.png)


Next: 2.4 split Cholesky 分解を用いる方法
Up: 2 標準固有値問題への帰着
Previous: 2.2 が正則な場合に使える、ある素朴な方法
桂田 祐史
2014-05-27
![]() が正定値 (実対称で固有値がすべて正) である場合、Cholesky 分解
が正定値 (実対称で固有値がすべて正) である場合、Cholesky 分解
![]() のことをしばしば
のことをしばしば ![]() と書く人が多い
(個人的には悪趣味だと感じているが)。
と書く人が多い
(個人的には悪趣味だと感じているが)。
![]() が実対称であれば、
が実対称であれば、
![]() も実対称である。
これは次の補題から分かる。
も実対称である。
これは次の補題から分かる。
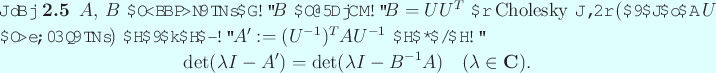
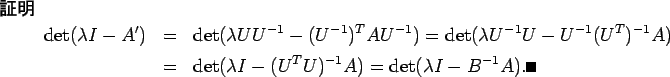

![]() の標準固有値問題については、
Rayleigh 商
の標準固有値問題については、
Rayleigh 商
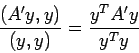
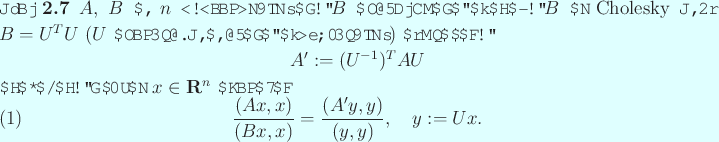
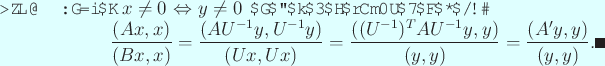

![\begin{jremark}[数値計算する上での注意]
ただし、
$A$, $B$ が�...
...��夫が有用である。
後述の Lanczos 法の節を見よ。
\end{jremark}](img53.png)