

Next: 2.2 が正則な場合に使える、ある素朴な方法
Up: 2 標準固有値問題への帰着
Previous: 2 標準固有値問題への帰着
一般固有値問題をそれと同値な標準固有値問題に変換する方法は、
以下紹介するように色々ある。
標準固有値問題の解法として、
Householder 法のように行列の成分が直接必要なアルゴリズムを利用する場合には、
行列の疎性が保存されるかどうかが重要なポイントになる。
これに対して、
冪乗法や Lanczos 法を利用する場合には、
行列の疎性は必ずしも必要ではない。つまり掛け算
を効率的に行うのに必ずしも 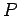 の疎性は必要ないことに注意しよう。
の疎性は必要ないことに注意しよう。
と分解できたとして、各 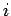 につき、
につき、
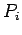 または
または 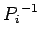 の一方が疎であれば良いわけである1。
の一方が疎であれば良いわけである1。


Next: 2.2 が正則な場合に使える、ある素朴な方法
Up: 2 標準固有値問題への帰着
Previous: 2 標準固有値問題への帰着
桂田 祐史
2014-05-27