- ... の一方が疎であれば良いわけである1
- つまり、
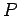 と
と 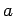 から
から 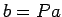 を計算するとき、
を計算するとき、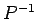 が疎であるならば、
連立1次方程式
が疎であるならば、
連立1次方程式 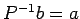 を解くことによって
を解くことによって 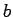 を求める、
という手順が採用できる。
を求める、
という手順が採用できる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
の重複度によって定義する2
- 微少な変形をすることによっても
定義できる?もっとも
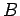 が正則でないような場合まで含めて
素朴に考えるのはきっと危険だ。
が正則でないような場合まで含めて
素朴に考えるのはきっと危険だ。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 3
3
- しかし、
まったく役に立たないというわけではない。
ずっと以前、某先生の卒研の学生が加藤敏夫先生の変分法の解説を勉強していて、
微分方程式の固有値問題の数値計算に取り組んでいたとき、
結局は Mathematica で $(I-B^-1A)=0$ を解くのが一番だった、
ということがあった。
「I君の固有値問題」 (http://nalab.mind.meiji.ac.jp/~mk/labo/text/eigen-I.pdf) を見よ。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.