

Next: A..4 misc
Up: A. 雑題
Previous: A..2 Rayleigh 商と min-max
Cholesky 分解については桂田 [7] を見よ。
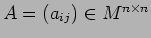 が上三角行列であるとは、
対角線より下にあるすべての成分が
が上三角行列であるとは、
対角線より下にあるすべての成分が 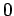 , つまり
, つまり
を満たすことをいう。
与えられた 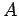 に対して、
(7) を満たす
に対して、
(7) を満たす 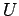 を
求めることを「
を
求めることを「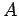 を Cholesky 分解する」
という。
を Cholesky 分解する」
という。



Next: A..4 misc
Up: A. 雑題
Previous: A..2 Rayleigh 商と min-max
桂田 祐史
2014-05-27
![]() が上三角行列であるとは、
対角線より下にあるすべての成分が
が上三角行列であるとは、
対角線より下にあるすべての成分が ![]() , つまり
, つまり
![\begin{jproposition}[正値対称行列の Cholesky 分解の存在]
$A\in\R^{n...
...0$ であるものに限ると $U$ は一意的である。
\end{jproposition}](img121.png)
![]() に対して、
(7) を満たす
に対して、
(7) を満たす ![]() を
求めることを「
を
求めることを「![]() を Cholesky 分解する」
という。
を Cholesky 分解する」
という。
![\begin{jproposition}[正値対称行列の平方根]
$A\in\R^{n\times n}$ が�...
...aymath}を満たす正値対称行列 $B$ が存在する。
\end{jproposition}](img122.png)
