

Next: A..3 正値対称行列, Cholesky 分解
Up: A. 雑題
Previous: A..1 ノルム
桂田 [7] を見よ。
前項に引き続き行列 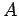 のスペクトル半径を
のスペクトル半径を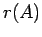 と書くことにする。
と書くことにする。
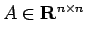 ,
, 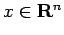 ,
, 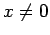 とするとき、
とするとき、
を 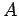 の
の 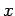 に対する Rayleigh 商と呼ぶ。
(
に対する Rayleigh 商と呼ぶ。
(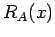 という記号はここだけのものである。)
という記号はここだけのものである。)
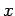 が
が 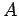 の固有値
の固有値 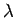 に属する
固有ベクトルならば、
に属する
固有ベクトルならば、
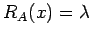 である。
である。
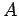 と
と 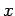 が与えられたとき、
が与えられたとき、
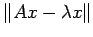 を最小にする
を最小にする 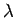 は
は 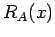 である。
である。
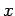 が
が 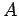 の固有値
の固有値 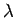 に属する固有値ベクトルに近いとき、
に属する固有値ベクトルに近いとき、
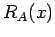 は
は 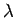 の良い近似値となる
(ここには書かないが具体的な評価式が得られる)。
の良い近似値となる
(ここには書かないが具体的な評価式が得られる)。
(厳密には命題の後半を min-max 原理という。
証明については例えば???を見よ。)


Next: A..3 正値対称行列, Cholesky 分解
Up: A. 雑題
Previous: A..1 ノルム
桂田 祐史
2014-05-27
![]() のスペクトル半径を
のスペクトル半径を![]() と書くことにする。
と書くことにする。
![]() ,
, ![]() ,
, ![]() とするとき、
とするとき、
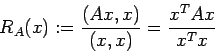
![\begin{jproposition}[min-max 原理]
$A\in\R^{n\times n}$ が対称である�...
...=\lambda_{n-j+1}
\quad\mbox{($1\le j\le n$)}.
\end{eqnarray*}\end{jproposition}](img117.png)