

Next: についての固有値問題の解法
Up: 4 Lanczos 法
Previous: 標準固有値問題への帰着
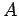 ,
, 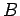 が帯行列であっても、
が帯行列であっても、
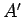 が疎性を持つことは期待できないが、
任意に与えられた
が疎性を持つことは期待できないが、
任意に与えられた 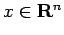 に対して、
に対して、
を計算するのは簡単である。
帯三角行列 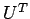 ,
, 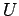 の掛け算は容易であるし、
の掛け算は容易であるし、
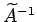 の掛け算
の掛け算 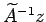 は
対称帯行列係数の連立1次方程式
は
対称帯行列係数の連立1次方程式
を解くことであるから、
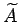 を Cholesky 分解しておけば非常に効率的に計算可能である。
したがって Lanczos 法に現れる計算は楽である。
を Cholesky 分解しておけば非常に効率的に計算可能である。
したがって Lanczos 法に現れる計算は楽である。


Next: についての固有値問題の解法
Up: 4 Lanczos 法
Previous: 標準固有値問題への帰着
桂田 祐史
2014-05-27