- ... 「常識的」で1
- 単振動については、
『単振動の数学的解析』
(http://nalab.mind.meiji.ac.jp/~mk/keisanki2/simple-harmonic-motion/)
という解説を書いたことがある。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
楕円関数、楕円積分というものが必要になる2
- 楕円積分、
楕円関数については、内輪向けだが、
『πノート
(http://nalab.mind.meiji.ac.jp/~mk/labo/text/pi.pdf)
というのを書いた。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
(戻ってきた時、前と同じ速さであり、減衰したりはしない3
- 厳密に証明するには、
途中で止まらないことを言う必要があるけれど、それは明らかでしょう。
注意が必要なのは、
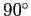 以下の触れの範囲の (
以下の触れの範囲の (
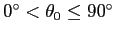 として、
として、
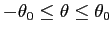 の範囲を行ったり来たりする)
「普通の」振り子以外に、
の範囲を行ったり来たりする)
「普通の」振り子以外に、
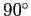 より大きな触れの範囲の振り子
(
より大きな触れの範囲の振り子
(
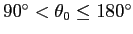 -- あまり現実的ではない?) や、
鉄棒の大車輪のようなぐるぐる回る振り子
(これはリアリティがあるけれど、「振り子」という名前に相応しくない?)
などの現象が方程式に含まれていることである。
-- あまり現実的ではない?) や、
鉄棒の大車輪のようなぐるぐる回る振り子
(これはリアリティがあるけれど、「振り子」という名前に相応しくない?)
などの現象が方程式に含まれていることである。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... で書き直しておこう4
- ぐるぐる回る大車輪似の「振り子らしくない」振り子では、
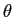 の最大値が存在しない。
そういう場合は考えない、ということにしておく。
この文書の議論は、
色々な本に載っているものを適当にブレンドしたものではあるけれど、
なかなかすっきりしないですねぇ。
の最大値が存在しない。
そういう場合は考えない、ということにしておく。
この文書の議論は、
色々な本に載っているものを適当にブレンドしたものではあるけれど、
なかなかすっきりしないですねぇ。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.