Next: 2.5 уиџтъІжЃетѕєуЕ║жќЊсЂИсЂ«ТГБт░ётй▒ (1) Up: 2. сЂ«тєЁуЕЇсЂеУдфсЂЌсѓѓсЂє Previous: 2.3 сЂ« Euclid сЃјсЃФсЃа
![\begin{jdefinition}[уЏ┤С║ц]
$(\cdot,\cdot)$\ сѓњ $\R^n$\ сЂ« Euclid тєЁуЕЇсЂесЂ...
...ђЂсЂЊсѓїсѓњ $M$\ сЂ«\textbf{уЏ┤С║ц}сЂетЉ╝сЂХсђѓ
\end{enumerate}\end{jdefinition}](img10.gif)
|
С╗ЦСИІсђЂт«џуЙЕсЂІсѓЅу░АтЇўсЂФсЃЂсѓДсЃЃсѓ»сЂДсЂЇсѓІТђДУ│фсѓњсЂѓсЂњсѓІсђѓ

|
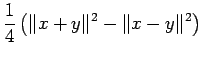 |
![$\displaystyle \frac{1}{4}
\left\{
\left[(x,x)+(x,y)+(y,x)+(y,y)\right]
-\left[(x,x)-(x,y)-(y,x)+(y,y)\right]
\right\}$](img72.png) | ||
![$\displaystyle \frac{1}{2}\left[(x,y)+(y,x)\right]
=(x,y).$](img73.png) |
сЂЊсЂ«сЂесЂЇ
сЂЎсЂфсѓЈсЂА
![]() сЂ«уЏ┤С║цсЂФсЂцсЂёсЂдсЂ»сђЂ
сЂ«уЏ┤С║цсЂФсЂцсЂёсЂдсЂ»сђЂ
![]() сЂї
сЂї ![]() сЂ«уиџтъІжЃетѕєуЕ║жќЊ
сЂ«уиџтъІжЃетѕєуЕ║жќЊ ![]() сЂДсЂѓсѓІсЂесЂЇсЂїуЅ╣сЂФжЄЇУдЂсЂДсЂѓсѓІсђѓ
сЂЊсЂ«сЂесЂЇсЂ»
сЂДсЂѓсѓІсЂесЂЇсЂїуЅ╣сЂФжЄЇУдЂсЂДсЂѓсѓІсђѓ
сЂЊсЂ«сЂесЂЇсЂ» ![]() сѓњ
сѓњ ![]() сЂ«уЏ┤С║цУБюуЕ║жќЊсЂетЉ╝сЂХсЂЊсЂесЂїтцџсЂёсђѓ
сЂЊсѓїсЂ»тЙїсЂДУе╝ТўјсЂЎсѓІсѓѕсЂєсЂФ
сЂ«уЏ┤С║цУБюуЕ║жќЊсЂетЉ╝сЂХсЂЊсЂесЂїтцџсЂёсђѓ
сЂЊсѓїсЂ»тЙїсЂДУе╝ТўјсЂЎсѓІсѓѕсЂєсЂФ
![]() сЂїТѕљсѓіуФІсЂцсЂІсѓЅсЂДсЂѓсѓЇсЂєсђѓ
сЂїТѕљсѓіуФІсЂцсЂІсѓЅсЂДсЂѓсѓЇсЂєсђѓ
СЙІсЂѕсЂ░ ![]() сЂДУђЃсЂѕсѓІсЂесЂЇсђЂ
сЂДУђЃсЂѕсѓІсЂесЂЇсђЂ
![]() сЂїуЏ┤уиџ (
сЂїуЏ┤уиџ (![]() ТгАтЁЃжЃетѕєуЕ║жќЊ) сЂ«сЂесЂЇ
ТгАтЁЃжЃетѕєуЕ║жќЊ) сЂ«сЂесЂЇ ![]() сЂ»т╣│жЮбсЂДсђЂ
сЂ»т╣│жЮбсЂДсђЂ
![]() сЂїт╣│жЮб (
сЂїт╣│жЮб (![]() ТгАтЁЃжЃетѕєуЕ║жќЊ) сЂ«сЂесЂЇ
ТгАтЁЃжЃетѕєуЕ║жќЊ) сЂ«сЂесЂЇ ![]() сЂ»уЏ┤уиџсЂФсЂфсѓІсђѓ
сЂ»уЏ┤уиџсЂФсЂфсѓІсђѓ
![]() сЂїтцДсЂЇсЂёсЂ╗сЂЕ
сЂїтцДсЂЇсЂёсЂ╗сЂЕ ![]() сЂїт░ЈсЂЋсЂёсЂЊсЂесЂ»ТЌбсЂФУе╝ТўјсЂЌсЂЪсЂ«сЂДсђЂ
ТгАсЂ«тЉйжАїсЂїТѕљсѓіуФІсЂцсЂЊсЂесЂ»т«╣ТўЊсЂФТЃ│тЃЈсЂДсЂЇсѓІсЂДсЂѓсѓЇсЂєсђѓ
сЂїт░ЈсЂЋсЂёсЂЊсЂесЂ»ТЌбсЂФУе╝ТўјсЂЌсЂЪсЂ«сЂДсђЂ
ТгАсЂ«тЉйжАїсЂїТѕљсѓіуФІсЂцсЂЊсЂесЂ»т«╣ТўЊсЂФТЃ│тЃЈсЂДсЂЇсѓІсЂДсЂѓсѓЇсЂєсђѓ
|
|
Уе╝ТўјсЂФсЂ»т░ЉсЂЌТ║ќтѓЎсЂїсЂёсѓІсЂ«сЂДтЙїсЂФтЏъсЂЎсђѓ
![\begin{yodan}[ТўћУЕ▒]
сђїСИГуиџт«џуљєсђЇсЂ»ТЌЦТюгсЂ«СИГтГджФўТаАсЂДсЂ»сђї\Ruby{...
...Є│сЂБсЂЪсђѓ
УДБТъљт╣ЙСйЋсЂ«теЂтіЏсЂ»тцДсЂЌсЂЪсѓѓсЂ«сЂДсЂѓсѓІсђѓ \qed
\end{yodan}](img13.gif)
сЂЊсЂ«тЉйжАїсЂІсѓЅсђЂСЙІсЂѕсЂ░ТгАсЂ«жЄЇУдЂсЂфТђДУ│фсЂїтЙЌсѓЅсѓїсѓІсђѓ
|
|
сЂеСИђУЄ┤сЂЎсѓІсЂЊсЂесЂїтѕєсЂІсѓІсЂ«сЂДсђЂт«ЪсЂ»уГЅтЈисЂїТѕљсѓіуФІсЂцсђѓ

|
ТАѓућ░ уЦљтЈ▓