良く知られているので省略。例えば杉浦 [#!______!#] を見よ。
帰納法による。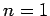 のときは明らか。
のときは明らか。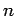 のとき成立すると仮定する。
のとき成立すると仮定する。
であり、
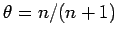 とおくと
とおくと
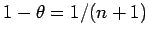 となることに注意すると、
凸性の仮定から、
となることに注意すると、
凸性の仮定から、
|
(1) |
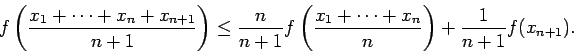 |
帰納法の仮定
を使って
特に 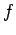 が狭義凸の場合は、(1) で等号が成り立つ
ための必要十分条件として、
が狭義凸の場合は、(1) で等号が成り立つ
ための必要十分条件として、
|
(3) |
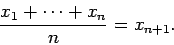 |
また (2) で等号が成り立つための必要十分条件として、
|
(4) |
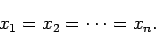 |
結局 (2) で等号が成り立つには
(3) と
(4) が同時に成り立つこと、すなわち
であることが必要十分である。
桂田 祐史
2017-04-30
![\begin{jdefinition}[凸関数, 狭義凸関数]
$\R$ の区間 $I$ で定義�...
...th}を満たすとき、$f$ は狭義凸であるという。
\end{jdefinition}](img2.png)
![\begin{jproposition}[2階導関数の符号と凸性]\upshape
$\R$ の区間�...
...��。
また $f''>0$ ならば $f$ は狭義凸である。
\end{jproposition}](img3.png)
