Next: B..2 実装 Up: B. Landen変換 Previous: B. Landen変換
![\begin{jproposition}[本当かな??]
$0<k<1$ に対して、
\begin{displa...
...qrt{(1-t^2)(1-k_1^2t^2)}}
\end{displaymath}が成り立つ。
\end{jproposition}](img434.gif)
|
![]() より
より
![]() であるから、
であるから、
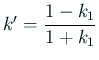 であり、
であり、

 (
(
また
 | ||
 |
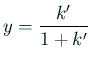 で最大であり、
で最大であり、
積分が等しいことは、、、、 ![]()
![]()
これを帰納的に繰り返すと
![]() は単調減少数列になるが、
実は非常に速く 0 に近づく。そこで
は単調減少数列になるが、
実は非常に速く 0 に近づく。そこで ![]() が十分小さくなったところで、
楕円積分を冪級数展開して計算することも考えられる。
実は算術幾何平均アルゴリズムを用いると、より効率の良い計算が可能である。
が十分小さくなったところで、
楕円積分を冪級数展開して計算することも考えられる。
実は算術幾何平均アルゴリズムを用いると、より効率の良い計算が可能である。
|
|
![]() より
より
![]() であるから、
であるから、
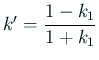 であり、
であり、

(27) の証明
![]() であるから、
であるから、
![]() から
から ![]() に下ろした垂線を
に下ろした垂線を ![]() とするとき、
とするとき、
(28) の証明
![]() ,
,
![]() であるから、
であるから、
 | ||
 | ||
 | ||
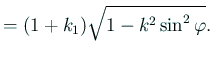 |
(29) の証明
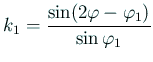
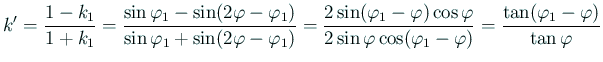
![]() を Landen 変換と呼ぶ。
を Landen 変換と呼ぶ。
順方向 (![]() から
から![]() を求める) には (29)
を使い、
逆方向 (
を求める) には (29)
を使い、
逆方向 (![]() から
から![]() を求める) には (27)
を使うのが便利そうだ。
を求める) には (27)
を使うのが便利そうだ。

|
 . すなわち
. すなわち  が成り立つ。
が成り立つ。
0 以上の整数 ![]() に対して、
に対して、
 が成り立っているならば、
が成り立っているならば、

 | ||
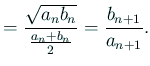 |
 が成立する。
が成立する。
ゆえに


 が成り立つ。
が成り立つ。
 | ||
 | ||
 |
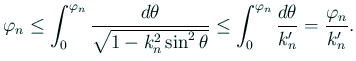
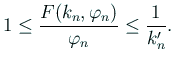


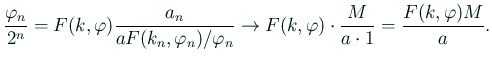
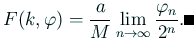
桂田 祐史