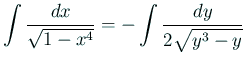Next: 2.2 標準形 Up: 2 楕円積分 Previous: 2 楕円積分

![]() の多項式
の多項式 ![]() と、有理式
と、有理式 ![]() について、
積分
について、
積分
![]() の次数が
の次数が ![]() 以下であれば、初等関数で表せる (??)。
以下であれば、初等関数で表せる (??)。
![]() の次数が
の次数が ![]() 以上であれば、
例外的な場合を除いて初等関数では表せない。
以上であれば、
例外的な場合を除いて初等関数では表せない。
![]() の次数が
の次数が ![]() ,
, ![]() であるとき、
積分 (1) を楕円積分
(elliptic integral) と呼ぶ。
であるとき、
積分 (1) を楕円積分
(elliptic integral) と呼ぶ。
![]() の次数が
の次数が ![]() 以上であるときは、
超楕円積分 (hyper-elliptic integral) と呼ぶ。
以上であるときは、
超楕円積分 (hyper-elliptic integral) と呼ぶ。
![]() の次数が
の次数が ![]() ,
, ![]() の場合を同列に論じるのは、
簡単な変数変換で相互に変換できるからである (そうだ)。
例えば
の場合を同列に論じるのは、
簡単な変数変換で相互に変換できるからである (そうだ)。
例えば