

Next: 18.3 高藤 康孝「偏微分方程式の固有値問題」
Up: 18 1997年度卒研
Previous: 18.1 北村 道介 「熱方程式に対する陽解法とCrank-Nicolson法の計算量と誤差」
~ee48001/sotu.dvi にある。
熱方程式の初期値境界値問題を差分法で解く場合、
空間次元が 1 ならば明らかに陽解法よりも陰解法が有利であるが、
空間次元が 2 の場合はそうとは言い切れない。
それについて考察した。
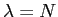 ,
,
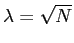 として、効率を追求している。
後輩に引き継いでもらいたい課題である。
として、効率を追求している。
後輩に引き継いでもらいたい課題である。


Next: 18.3 高藤 康孝「偏微分方程式の固有値問題」
Up: 18 1997年度卒研
Previous: 18.1 北村 道介 「熱方程式に対する陽解法とCrank-Nicolson法の計算量と誤差」
桂田 祐史
2015-12-24
![]() ,
,
![]() として、効率を追求している。
後輩に引き継いでもらいたい課題である。
として、効率を追求している。
後輩に引き継いでもらいたい課題である。