next up previous
Next: 60 qolibri Up: 2024年のコンピューターノウハウ (Mac) Previous: 58 Ghostscriptの文字化けを直す

59 Fresnel積分の数値計算再び (ライブラリィ探し)

前年度に Fresnel 積分

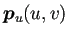
$\displaystyle C(x)=\int_0^x \cos(t^2)\D t,\quad S(x)=\int_0^x \sin(t^2)\D t,\quad $

の数値計算の話題を書いたけれど (「Fresnel 積分の数値計算 (あまりMacと関係ない)」)、 2024年度の卒研で Clothoid をテーマにした学生が出て (元々微分幾何のネタでやっていたので、 Frenet-Serret の公式を常微分方程式とみなして解くとか、

$\displaystyle C'(x)=\cos(x^2),\quad C(0)=0,\quad S'(x)=\sin(x^2),\quad S(0)=0 $

を微分方程式とみなして解くとか、いろいろな方法で計算してくれた)、 Fresnel積分の数値計算を考えることになった。

繰り返しになるが、Mathematica, Python, Julia などでは正規化 Fresnel 積分

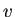
$\displaystyle C_{\text{n}}(x)=\int_0^x \cos(\pi t^2)\D t,\quad S_{\text{n}}(x)=\int_0^x \sin(\pi t^2)\D t,\quad $

が用意されている ( $ C_{\text{n}}$, $ S_{\text{n}}$ はここだけの記号)。

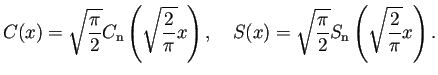
$\displaystyle C(x)=\sqrt{\frac{\pi}{2}}C_{\text{n}}\left(\sqrt{\frac{2}{\pi}}x\... ...quad S(x)=\sqrt{\frac{\pi}{2}}S_{\text{n}}\left(\sqrt{\frac{2}{\pi}}x\right). $

$\displaystyle C_{\text{n}}(1)=0.779893\cdots,\quad S_{\text{n}}(1)=0.438259\cdots,\quad C(1)=0.904524\cdots,\quad S(1)=0.310268\cdots. $

Mathematica で確認
In[] := mys[x_]:=Sqrt[Pi/2]FresnelS[Sqrt[2/Pi]x]
In[] := myc[x_]:=Sqrt[Pi/2]FresnelC[Sqrt[2/Pi]x]
In[] := {FresnelC[1.0],FresnelS[1.0]}
Out[] = {0.779893, 0.438259}
In[] := {myc[1.0],mys[1.0]}
Out[] = {0.904524, 0.310268}

C には、Cで書かれたプログラム (これも正規化 Fresnel 積分を計算する) が公開されている (NETLIB で入手できる cephes に含まれている)。

まあ、それでとりあえずの用は足りるけれど、 古めかしいプログラムのお世話になるのではなく、 最近の整備されたのを利用できると良いかも、と考えて少し調べてみた。

C++だと、Boost クラス・ライブラリィに特殊関数が含まれているはずだ、 ということで Boost を調べたのだけれど、Fresnel積分は入ってなかった。

Abramowitz-Stegun [#!Abramowitz-Stegun!#] によると、 Fresnel積分は誤差関数 $ \mathop{\mathrm{erf}}\nolimits $ の親戚扱いをされている。 実際、$ erf$ を使って Fresnel 積分を表すことができる。

$\displaystyle C(z)=\frac{\pi}{4} \left[ \sqrt{-i}\;\mathrm{erf}\left(\sqrt{i}... ...\frac{1+i}{\sqrt{2}}\mathrm{erf}\left(\frac{1-i}{\sqrt{2}}z\right) \right] , $

$\displaystyle S(z)=\frac{\pi}{4} \left[ \sqrt{i}\;\mathrm{erf}\left(\sqrt{i}z... ...\frac{1-i}{\sqrt{2}}\mathrm{erf}\left(\frac{1-i}{\sqrt{2}}z\right) \right] . $

件の学生は、この公式を使って Fresnel 積分を計算するコードを作成した。 おお、なるほど。馬力がありますね、

学生は Python でやったのだけれど、効率とか調べたいので、C++でやってみるか、 と思い立った。誤差関数ならば Boost にも入っているはずだ …ところが残念なことに Boost の誤差関数は実数引数にしか対応していない。

複素引数の特殊関数が欲しい、という人は検索するとすぐ出て来るのだけれど (当たり前だよね)、 そういう要求って出てなかったなあ、とか言う反応があったり。 やはり複素数計算はなんとなく袖にされがちなのか。

そう考えると、Python の誤差関数が複素引数に対応しているって、 すごいなあ、と感心した。

さて、どうしよう？

ふと、ChatGPT 様にお伺いを立ててみよう、と浮かんだ。 色々なアイディアを出してくれたが、自分が思いつかなかったものが一つ。

曰く、Faddeeva function を使え。

Wikipedia の Faddeeva function を見る (ちなみに日本語バージョンは存在しない)。

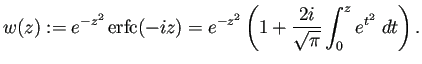$\displaystyle w(z):=e^{-z^2}\mathop{\mathrm{erfc}}\nolimits (-iz) =e^{-z^2}\left(1+\frac{2i}{\sqrt{\pi}}\int_0^z e^{t^2}\;\D t\right).$ (1)

ACM Transactions on Mathematical Softwareに に2つのアルゴリズムと実装が発表されているそうである。

MITライセンスで利用できる実装 libcerf がある。

さらに同じ MIT で The Faddeeva Package というのもある。こちらでやってみるか。 
curl -O http://ab-initio.mit.edu/Faddeeva.cc
curl -O http://ab-initio.mit.edu/Faddeeva.hh
c++ -O -c Faddeeva.cc
Cバージョンもあるみたい (中で include していたりする)。 
curl -O http://ab-initio.mit.edu/Faddeeva.c
curl -O http://ab-initio.mit.edu/Faddeeva.h
cc -O -c  Faddeeva.c

Faddeeva パッケージの中に $ \mathop{\mathrm{erf}}\nolimits $ を計算する関数が含まれているので、 私の目的にはそれを呼び出せば良い。

testfaddeeva.cpp

/*
 * testfaddeeva.cpp
 * http://ab-initio.mit.edu/faddeeva/
 *  curl -O http://ab-initio.mit.edu/Faddeeva.cc
 *  curl -O http://ab-initio.mit.edu/Faddeeva.hh
 *  c++ -O -c Faddeeva.cc
 *  c++ -O -o testfaddeeva testfaddeeva.cpp Faddeeva.o
 * 2020 MacBook Air (M1) で 6.21 秒
 */

#include <iostream>
#include <iomanip>
#include "Faddeeva.hh"

using namespace std;
using namespace Faddeeva;

double sqr_pi_4, sqr_pi_2;
complex<double> sqrt_i, sqrt_mi;

complex<double> C(complex<double> z)
{
  return sqr_pi_4 * (sqrt_mi * erf(sqrt_i * z,0.0) + sqrt_i * erf(sqrt_mi * z,0.0));
}

complex<double> S(complex<double> z)
{
  return sqr_pi_4 * (sqrt_i * erf(sqrt_i * z,0.0) + sqrt_mi * erf(sqrt_mi * z,0.0));
}

// 変数が実数の場合、2つの erf() は共役複素数なので、1つだけ計算すれば良い。
void set_CS(double &c, double &s, double x)
{
#ifdef OLD
  complex<double> w, wconj;
  // cout << w << endl;
  w=sqr_pi_4 * erf(sqrt_i * x, 0.0);
  wconj = conj(w);
  c = real((sqrt_mi * w + sqrt_i * wconj)); // c = 2 * real(sqrt_mi * w);
  s = real((sqrt_i * w + sqrt_mi * wconj)); // s = 2 * real(sqrt_i * w);
#else
  complex<double> w;
  w=sqr_pi_2 * erf(sqrt_i * x, 0.0);
  c = real(sqrt_mi * w);
  s = real(sqrt_i * w);
#endif
}

int main(void)
{
  int i, n, method = 1;
  double a, b, x, dx;
  complex<double> I(0.0,1.0);
  sqrt_i = sqrt(I); sqrt_mi = sqrt(-I);
  sqr_pi_4 = sqrt(4 * atan(1.0)) / 4;
  sqr_pi_2 = sqrt(4 * atan(1.0)) / 2;
  cout << sqrt_i << " " << sqrt_mi << " " << sqr_pi_4 << endl;

  a = 0.0; b = 1.0;
  n = 100000000;
  dx = (b - a) / n;
  if (method == 0) {
    for (i = 0; i <= n; i++) {
      x = a + i * dx;
      cout << fixed << setprecision(3) << x << " "
	   << scientific << setprecision(15)
	   << C(x).real() << " " << S(x).real() << endl;
    }
  }
  else {
    for (i = 0; i <= n; i++) {
      double c, s;
      x = a + i * dx;
      set_CS(c, s, x);
#ifdef NONE
      cout << fixed << setprecision(3) << x << " "
	   << scientific << setprecision(15)
	   << c << " " << s << endl;
#endif
    }
  }

  x = 1000.0;
  printf("x=%f, c=%18.15e, s=%18.15e\n", x, C(x).real(), S(x).real());
  return 0;
}

(20253/7追記) 関数ごとにこういう探索を繰り返すのは、暇つぶしには良いけれど、 何か間違えているような気がする。 「面白そうだけどそのうちに」と考えていて放置してあるものをチェックするのかな。


桂田 祐史