2 メネラウスの定理 (1) 覚え方

(2025/3/25)

メネラウスの定理は、私が高校生の頃の教科書には載っていなかった (と思う。余り記憶に自信はないけれど。)。近年は、数学Aの教科書に載っていて、そのせいで別件でパラパラしているときに目にはするけれど、あまりピンと来ない定理だった。

以前一度覚えようと思ったことがあったが、挫折した。普段使わないから定着しないんだよね…と一人で言い訳をしたり。

この機会に再挑戦しよう。

図: 三角形 ABC の2辺 AB, CA と交わる直線 $\ell$ と、辺 BC の延長線との交点 D について

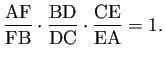
$\displaystyle \frac{\mathrm{AF}}{\mathrm{FB}}\cdot \frac{\mathrm{BD}}{\mathrm{DC}}\cdot \frac{\mathrm{CE}}{\mathrm{EA}}=1.$

しばらく眺める… ああ、なんだ、そういうことか。分数を英語流に分子・分母の順で読むことにすると、

$\displaystyle A,F,F,B,B,D,D,C,C,E,E,A$

と文字が2回ずつ連続する。点が現れる順番は、 BからCを通り越してDに飛んでから戻って来るところを除けば、位置としても順番である。多分、英語を使う人にとっては分かりやすい、というか、覚えやすく間違えにくい。分数を分母・分子の順に読む日本人にとっては、覚えにくくなっていると思う。幸い値は

なので、分母・分子を逆にして

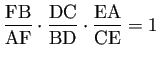
$\displaystyle \frac{\mathrm{FB}}{\mathrm{AF}}\cdot \frac{\mathrm{DC}}{\mathrm{BD}}\cdot \frac{\mathrm{EA}}{\mathrm{CE}}=1$

にすると良いのかな、と考えたりする (変な式と言われそうだ)。

この定理についての現存する最古の説明は、アレクサンドリアのメネラオス (70-140頃)の『球面論』に記載されているそうだ。そのためメネラウスの定理と呼ぶらしい。メネラオスは数学者かつ天文学者であった (若い頃アレクサンドリアにいて、後にローマに住んだ、とされている)。平面三角形で知られている定理を球面三角形に拡張して使った、ということらしい。実はメネラオスは球面三角法の先駆者である。この(平面三角形についての)定理をメネラオスが発見した、はじめて証明した、というわけではないみたい。とても有名なプトレマイオスのアルマゲストに天体観測の記録としてメネラオスが出て来るとか、アルマゲストでは球面天文学の多くの問題にこの定理(球面三角法版) を適用しているとか。プルタルコスの著述にメネラオスとルキウスとの会話が載っているとか。また、この定理はアラビア世界で詳しく研究されたとか。

これまでメネラウスの定理には余り関心が持てなかったのであるが、こういう背景を知ると、がぜん興味が沸いてきた (我ながら単純だ)。気が向いたら証明とかも調べてみよう (平面の場合に証明するのは簡単だけれど、球面三角形でもやるとなると、なんかアイディアが必要だろうね。)。

(2025/3/26追記) ネットで長崎[1] という論文を紹介しているのを見つけた。それによると、メネラウスの定理は以前は教えられていたが、昭和48年から教えられなくなった。また (これは [1] には書かれていないが)、平成に入って復活した、ということである。それを知って調べ始めてから分かったことであるが、定理の名前自体は学習指導要領には書かれていないようである。学習指導要領解説というのを見るべきらしい (学習指導要領は古いものもWWWにあるが、解説の方は古いのは置いてないのか)。

桂田祐史