「円周率の計算の歴史」 という文書もある。興味があれば見てみよう。
![]() の Maclaurin 展開
の Maclaurin 展開
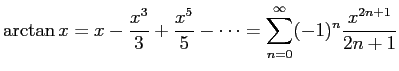
を用いて円周率
有名なのが ![]() とおいてできるマーダヴァ・グレゴリー・ライプニッツ級数
である:
とおいてできるマーダヴァ・グレゴリー・ライプニッツ級数
である:
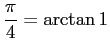 より
より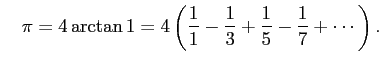
これは印象的であるが、 収束は極端に遅く、
絶対値の小さい ![]() を選ぶと実用的な公式が得られる。
例えば
を選ぶと実用的な公式が得られる。
例えば
![]() より
より
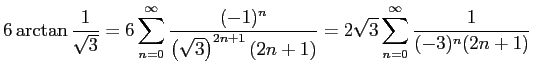 |
|||
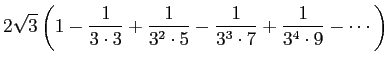 |
Abraham Sharp は ![]() 項まで足し合わせて、
小数点以下 100 桁以上の円周率の値を求めたという。
項まで足し合わせて、
小数点以下 100 桁以上の円周率の値を求めたという。
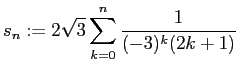
とおき、
s[n_]:=2 Sqrt[3]Sum[1/((-3)^k*(2k+1)),{k,0,n}]
s210=s[210]
N[s210,200]
s210-Pi
ns[n_]:=N[s[n],1000]
match[n_]:=-1.0*Log[10,Abs[ns[n]-Pi]]
ListPlot[Table[match[n],{n,210}]]
Remove[k,match,n,ns,s]
|
L. Euler (超有名数学者) は次の公式を 1737 年に得た。
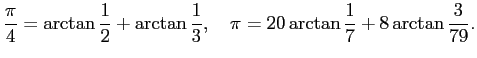
John Machin (1680-1752, ロンドン大学天文学教授) は
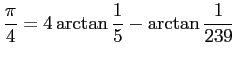
を用いて 100 桁の値を計算した。この公式は以後多くの人達に採用され続ける。 人手での
C. F. Gauss (数学界の巨人) は 1863 年に以下の公式を得た。
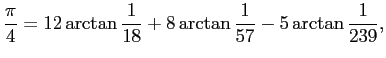
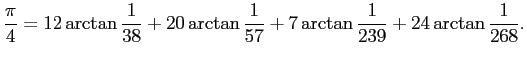
前者はおそらく 3 項の
2005年現在の最高記録は、 2002年12月、金田康正、うしろ後やすのり保範等の グループが達成した 1 兆 2400 億桁というものだが、 それは高野喜久雄の公式
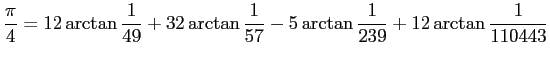
による (この話は WWW で検索すれば色々ヒットするので省略)。