B..5.1 LU 分解

最初に二つの言葉を定義する。

行列 $L=(\ell_{ij})$ が下三角行列 (lower triangluar matrix) であるとは、対角線の上にある成分がすべて 0 である、つまり

$$i>j\quad\Then\quad \ell_{ij}=0$$

が成り立つことと定義する。

同様に、 $U=(u_{ij})$ が上三角行列 (upper triangular matrix) であるとは、 対角線の下にある成分がすべて 0 である、つまり

$$i<j\quad\Then\quad u_{ij}=0$$

が成り立つことと定義する。

目で見えるように書くと

$$L= \left( \begin{array}{ccccc} \ell_{11} & 0 & \cdots&\cdots &... ... & u_{2n}\\ \vdots & 0 & \ddots & \\ 0 & 0 & & u_{nn} \end{array} \right)$$

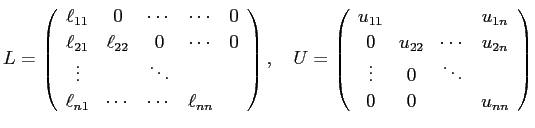
ということである。

LU 分解

行列 $A$ に対して、

$$A = L U$$

を満たす下三角行列 $L$ と上三角行列 $U$ を求めることを (これはいつもできるとは限らない -- 後述)、 $A$ を LU 分解すると呼ぶ。

Gauss の消去法の前進消去段階では、 係数行列に行に関する基本変形を施して上三角行列 (それを $U$ とおく) に 変形したが、 行に関する基本変形は、基本行列を左からかけることで表現できる。 Gauss の消去法では、これら基本行列はすべて正則な下三角行列である。 そこで、この変形は

$$L_k \cdots L_2 L_1 A = U$$   $$\mbox{($L_j$ は正則な下三角行列, $U$ は上三角行列)}$$

とかける。これから

$$A={L_1}^{-1}{L_2}^{-1}\cdots {L_k}^{-1}U$$

となるが、 $L:={L_1}^{-1}{L_2}^{-1}\cdots {L_k}^{-1}$ は実は下三角行列である。 これは次の補題から分かる。

さて、それでは Gauss の消去法はいつでも出来るかというと、 (掃き出し法との類推ですぐ分かるように) 対角成分に 0 が現われたらダメになるわけである。 この場合は、行を適当に交換することで消去が出来るようになる。

正則行列 $A$ の LU 分解はたとえ存在しても一意ではないが、 $A$ を

$$A = L D U\quad ($$$$\mbox{$L$ は対角成分が $1$ の下三角行列、 $U$ は対角成分が $1$ の上三角行列、 $D$ は対角行列}$$$$)$$

の形に分解する LDU 分解は一意である。