まず、正五角形を描くことを考えましょう。
与えられた自然数 ![]() に対して、
円周を
に対して、
円周を ![]() 等分する点の座標を表す式は、
あちこちで習っていますね。
一周
等分する点の座標を表す式は、
あちこちで習っていますね。
一周 ![]() を
を ![]() 等分した角は
等分した角は
![]() ですから、
ですから、
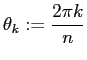
として、
とおくと、
簡単のため ![]() として、
また角度が分かりやすいように (?) 単位を度で表すことにして、
点の番号を 0
からでなく
として、
また角度が分かりやすいように (?) 単位を度で表すことにして、
点の番号を 0
からでなく ![]() から振ることにして、
また頂点をずらす角度
から振ることにして、
また頂点をずらす角度
![]() を導入して (真上に頂点が来ると星がきれい)
を導入して (真上に頂点が来ると星がきれい)
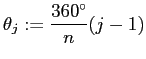 | ||
次のプログラムで正五角形の輪郭が描けます。
REM 正五角形を描く OPTION ANGLE DEGREES LET n=5 LET DT=360/n LET p=90 REM 頂点の座標を求める DIM x(n),y(n) FOR j=1 TO n t=(j-1)*DT+p PRINT t LET x(j)=COS(t) LET y(j)=SIN(t) NEXT j REM 正五角形を描く SET WINDOW -1,1,-1,1 FOR j=1 TO n PLOT LINES : x(j),y(j); NEXT j PLOT LINES : x(1),y(1) END |
正五角形の内部を塗るのは簡単で、 最後 (END行の前) に次の2行を加えるだけです。
SET AREA COLOR "red" MAT PLOT AREA : x,y |
| pentagon.BAS |
REM pentagon.BAS --- 正五角形を描く OPTION ANGLE DEGREES LET n=5 LET DT=360/n LET p=90 REM 頂点の座標を求める DIM x(n),y(n) FOR j=1 TO n LET t=(j-1)*DT+p PRINT t LET x(j)=COS(t) LET y(j)=SIN(t) NEXT j REM 頂点を順に結んで正五角形を描く SET WINDOW -1,1,-1,1 FOR j=1 TO n PLOT LINES : x(j),y(j); NEXT j PLOT LINES : x(1),y(1) REM 塗る SET AREA COLOR "red" MAT PLOT AREA: x,y END |