

Next: 2 レポート課題5B解説
Up: 1 方程式の数値解法
Previous: 1.8.3 とりあえずの結論
プログラムとその実行結果、
その説明の 3 点を含んだレポートを TEX を使って執筆し、
PDF ファイル kadai7.pdf を
Oh-o! Meiji レポートシステムを使って提出せよ。
締め切りは 6月12日 (火曜) 18:00 とします。
二分法、Newton 法のいずれかを用いること
(余裕があれば両方で解き比べてみること)。
以下、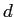 のところを、最初は
のところを、最初は 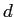 としていましたが、
例題プログラム中の区間
としていましたが、
例題プログラム中の区間 ![$ [a,b]$](img32.png) の
の 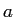 と名前が衝突して、
詰まらない混乱を招くので、変更しました
(2012年5月30日授業終了後の修正)。
と名前が衝突して、
詰まらない混乱を招くので、変更しました
(2012年5月30日授業終了後の修正)。
- (1)
- 与えられた正数
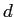 に対して
に対して 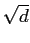 を計算するプログラムを作り、
を計算するプログラムを作り、
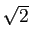 ,
, 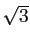 ,
, 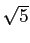 を計算し、
組込み関数 SQR() の結果と比較せよ。
出来れば 1000 桁演算モード (OPTION ARITHMETIC
DECIMAL_HIGH) でやってみよう。
を計算し、
組込み関数 SQR() の結果と比較せよ。
出来れば 1000 桁演算モード (OPTION ARITHMETIC
DECIMAL_HIGH) でやってみよう。
- (2)
- 与えられた
![$ d\in [-1,1]$](img97.png) に対して (普通の三角関数は利用してもよいが、
逆三角関数は利用せずに)
に対して (普通の三角関数は利用してもよいが、
逆三角関数は利用せずに)
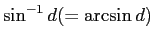 を計算するプログラムを作り、
を計算するプログラムを作り、
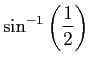 を計算し、
組込み関数 ASIN() の結果と比較せよ。
(これは普通の演算モードか、
OPTION ARITHMETIC NATIVE でやるのが良いでしょう。)
を計算し、
組込み関数 ASIN() の結果と比較せよ。
(これは普通の演算モードか、
OPTION ARITHMETIC NATIVE でやるのが良いでしょう。)
| ヒント |
- 紹介したサンプル・プログラム
(bisection.BAS, newton.BAS) を
書き直すという手順で作成できる。
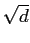 は例えば
は例えば 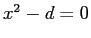 の正の解と解釈できる
(
の正の解と解釈できる
(
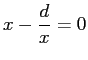 の解とする手もあるが…)。
の解とする手もあるが…)。
-
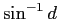 は
は
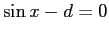 の実数解と解釈できる。
の実数解と解釈できる。
|


Next: 2 レポート課題5B解説
Up: 1 方程式の数値解法
Previous: 1.8.3 とりあえずの結論
桂田 祐史
2012-05-30
![]() のところを、最初は
のところを、最初は ![]() としていましたが、
例題プログラム中の区間
としていましたが、
例題プログラム中の区間 ![]() の
の ![]() と名前が衝突して、
詰まらない混乱を招くので、変更しました
(2012年5月30日授業終了後の修正)。
と名前が衝突して、
詰まらない混乱を招くので、変更しました
(2012年5月30日授業終了後の修正)。
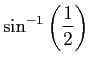 を計算し、
組込み関数 ASIN() の結果と比較せよ。
(これは普通の演算モードか、
OPTION ARITHMETIC NATIVE でやるのが良いでしょう。)
を計算し、
組込み関数 ASIN() の結果と比較せよ。
(これは普通の演算モードか、
OPTION ARITHMETIC NATIVE でやるのが良いでしょう。)