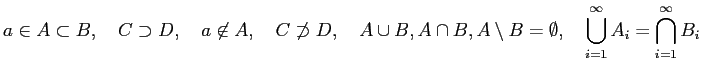
\[
a\in A\subset B,\quad
C\supset D,\quad
a\not\in A,\quad
C\not\supset D,\quad
A\cup B, A\cap B, A\setminus B=\emptyset,\quad
\bigcup_{i=1}^\infty A_i=\bigcap_{i=1}^\infty B_i
\]
|
|
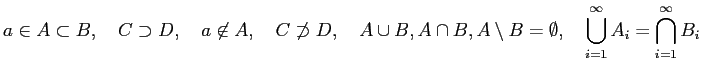
|
![]() (\in) の逆向きが
(\in) の逆向きが
![]() (\ni) であったり、
(\ni) であったり、
![]() (\subset) の逆向きが
(\subset) の逆向きが
![]() (\supset) であるのは、
苦し紛れっぽいけれど…
(\supset) であるのは、
苦し紛れっぽいけれど…