4 実験してみよう

1次元熱方程式を差分法で解いた。以下のことが分かった。

• $\theta=1$ (後退Euler法) であれば、 最大値ノルムの意味で無条件に安定であった。
• ノルムによっては
  • $\theta\ge 1/2$ であれば無条件安定になった。
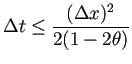  • $0<\theta<1/2$ のとき、 時間刻みが十分小さくない ( $\Delta t\le\dfrac{(\Delta x)^2} {2(1-2\theta)}$) と不安定になる。

heatT.edp で $\theta=1,1/2,1/4$ の場合に、 時間刻みを大きくしても安定性が保たれるか調べる。

[

l]キーボード入力が出来るように改造する

real Tmax=10, tau=0.01, t, theta=1; // thetaを加える。=1の時は実は後退Euler
// コメント・アウトすると、m, tau, theta が実行時に変更できるようになる
// cout << "m dt theta: "; cin >> m >> tau >> theta;
// cout << "m=" << m << ", tau=" << tau << ", theta=" << theta << endl;
mesh Th=square(m,m);

Tmax も大きめにしておくと分かりやすい。