2 Mathematica で Fourier 変換

Mathematica には、 FourierTransform[] とその逆変換 InverseFourierTransform[] が用意されている。 しかし、これをそのまま使っても、

$${\cal F}f(\xi)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty f(x)e^... ...F}^\ast g(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty g(\xi)e^{i\xi x}\D\xi$$

の計算は出来ない。

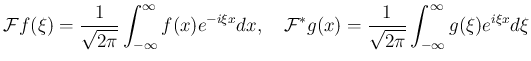
実は Fourier 変換の定義には、色々な流儀があり (本質的には同じものなのだが、定数因子など、細かいところが異なる)、 Mathematica のデフォールトは、 上の定義 (数学のテキストでは良くみかけるもので、N先生の講義でも採用されている) とは一致していない。

でも実は困らない。 Mathematica には、 そういう流儀の違いを解決するための賢い仕掛けが用意されていて、 この講義の流儀に従って Fourier 変換を計算させるには、

FourierParameters->{0,-1}

というオプションを与える 。

つまり、式 f[x] で表される関数の Fourier 変換を表す式 (変数を y とする) を求めるには次のようにする。

${\cal F}[f(x)](y)$ を求めるには

FourierTransform[f[x],x,y,FourierParameters->{0,-1}]

f[x_]:=Exp[-a x^2]
FourierTransform[f[x], x, y, FourierParameters-> {0, -1}]

g[x_]:=Exp[-a Abs[x]]
FourierTransform[g[x], x, y, FourierParameters-> {0, -1}]

h[x_]:=1/(x^2+a^2)
FourierTransform[h[x], x, y, FourierParameters-> {0, -1}, Assumptions->	a>0]

chi[x_, a_] := Boole[-a < x < a]/(2 a)
FourierTransform[chi[x,3], x, y, FourierParameters-> {0, -1}]

3つめの計算で、Mathematica は HeavisideTheta[] を用いて答える。 これはいわゆる Heaviside 関数

$$H(x):= \left\{ \begin{array}[tb]{ll} 1 & \text{($x\ge 0$)} \\ 0 & \text{($x<0$)} \end{array} \right.$$

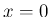と考えて良い (実は $x=0$ での値は定義していないので、 上の式とは厳密には異なる)。