Next: 1.2 部分和のグラフを描く Up: 1 Mathematica で Fourier級数 Previous: 1 Mathematica で Fourier級数
Mathematica には、積分を計算する Integrate[] があるので、 Fourier係数の計算に利用できる。
Simplify[Integrate[f[x]Cos[n x],{x,-Pi,Pi}]/Pi,Assumptions->Element[n,Integers]]
Simplify[Integrate[f[x],{x,-Pi,Pi}]/Pi]
Simplify[Integrate[f[x]Sin[n x],{x,-Pi,Pi}]/Pi,Assumptions->Element[n,Integers]]
|
ところで、Mathrematica には Fourier変換専用の関数が色々用意されている。 特にFourier級数を求めるためには
![]() は、FourierCoefficient[] ですぐに求められる。
は、FourierCoefficient[] ですぐに求められる。
関数 ![]() が偶関数あるいは奇関数である場合は、
が偶関数あるいは奇関数である場合は、![]() ,
, ![]() もすぐ求められる。
もすぐ求められる。
![]() が偶関数でも奇関数でもない場合に、
が偶関数でも奇関数でもない場合に、
![]() と
と ![]() をどうやって求めるかが問題となる。
をどうやって求めるかが問題となる。
| 方法1 |
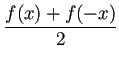 のFourier余弦係数, のFourier余弦係数,
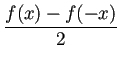 のFourier正弦係数であるので、 のFourier正弦係数であるので、
FourierCosCoefficient[(f[x]+f[-x])/2,x,n] FourierCosCoefficient[(f[x]+f[-x])/2,x,0] FourierSinCoefficient[(f[x]-f[-x])/2,x,n]とすれば求められる (順に |
| 方法2 |
|
公式
c[n_] := FourierCoefficient[f[x], x, n] Simplify[c[n] + c[-n], Assumptions -> n > 0] 2c[0] Simplify[I(c[n]-c[-n]), Assumptions -> n > 0]とすれば求められる。 |
Mathematica が、
一般の場合の ![]() ,
, ![]() を計算する関数を用意してくれれば良いのに、
と思うが、なぜこのような仕様になっているのだろう。
偶関数でも奇関数でもない場合には実際上使われないと考えているのだろうか?
(私には謎だ。)
を計算する関数を用意してくれれば良いのに、
と思うが、なぜこのような仕様になっているのだろう。
偶関数でも奇関数でもない場合には実際上使われないと考えているのだろうか?
(私には謎だ。)