9 複素対数関数を描く

2変数 $(x,y)$ の関数としての $\MyIm \Log (x+i y)$, $\MyRe \Log (x+i y)$ のグラフを描いてみよう。

それぞれ $\Arg (x+iy)$, $\log\sqrt{x^2+y^2}$ であるから、 コンピューターで図示しなくても分からなくはないが (図示しなくても分かるけれど)、 やってみることを勧める。

Plot3D[] や ContourPlot[] では、 描画範囲を $x$座標と$y$座標の範囲で指定するので、 変数は x+I y と書くと良い (小さなノウハウ)。

[

l]Mathrmatica でグラフを描こう Plot3D[Im[Log[x+I y]],{x,-2,2},{y,-2,2},
    RegionFunction->Function[{x,y,z},x^2+y^2<4]]

Plot3D[Re[Log[x+I y]],{x,-2,2},{y,-2,2},
    RegionFunction->Function[{x,y,z},x^2+y^2<4]]

RegionFunction[] は $x^2+y^2<4$ の範囲だけでグラフを描くための指定 (なくても描けるし、絞るのは趣味の問題)。

図: $\MyIm \Log(x+yi)$, $\MyRe \Log(x+yi)$ のグラフ

(以前は描画範囲を絞るため、 RegionFunction を使うのではなく、 Re[Log[x+I y]]Boole[x^2+y^2<4] のグラフを描いていた。)

Mathematica で描いたグラフは、 マウスでつかんでグリグリ動かせる。 ぜひやってみること (静止画を見るだけだと今ひとつ分かりにくい)。

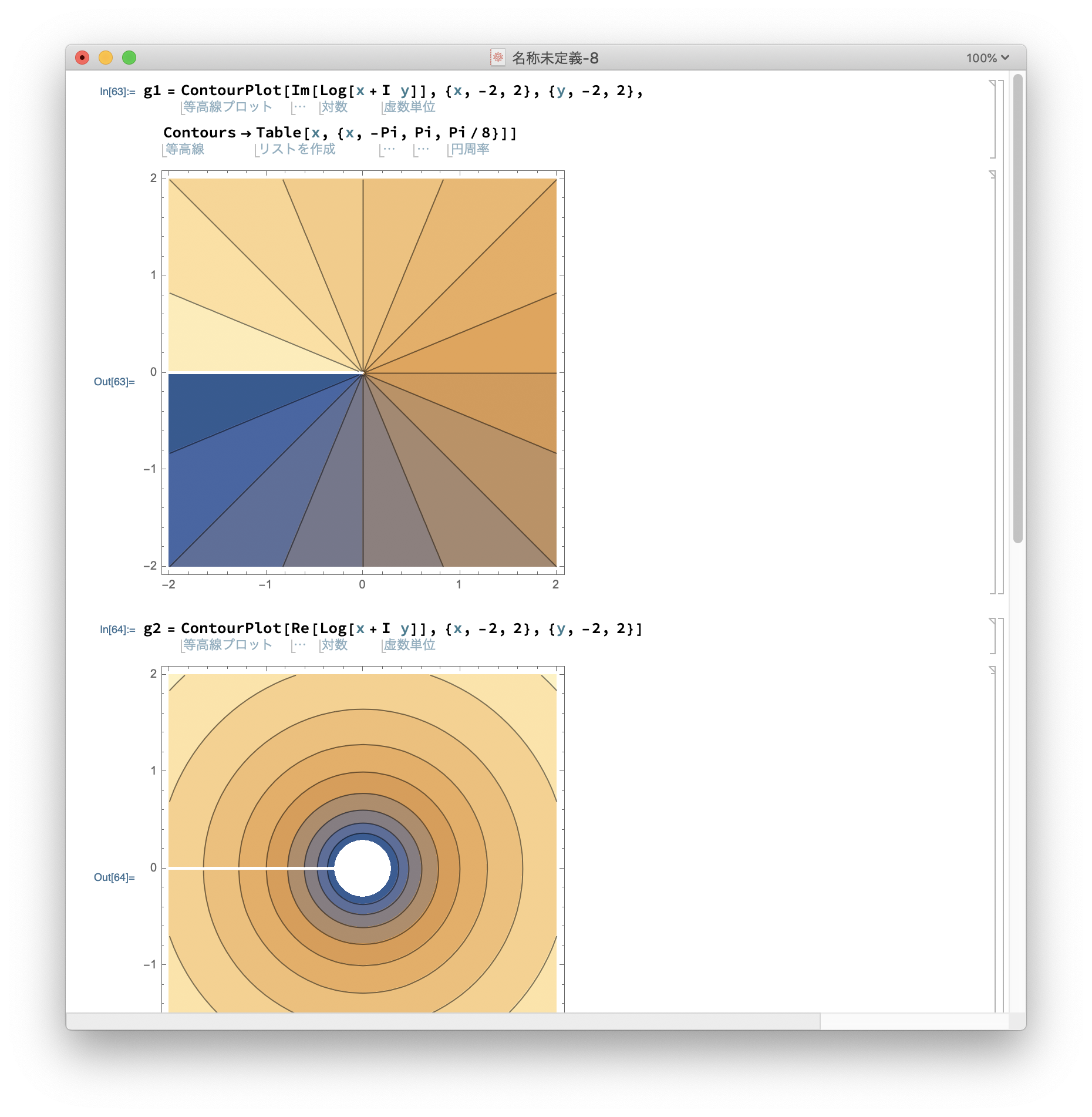
Plot3D[] の代わりに ContourPlot[] を用いると、 レベル表示 (≒等高線描画) 出来る。

ContourPlot[Im[Log[x+I y]], {x,-2,2}, {y,-2,2}, Contours->Table[x,{x,-Pi,Pi,Pi/8}]]

ContourPlot[Re[Log[x+I y]],{x,-2,2},{y,-2,2}]