l9g!"4JC1$J$b$N$K8B$i$l$k$N$G!"�(B
�$B652J=q$K$"$2$?Nc$r$h$/8+$F$*$/$H$h$$!#�(B
�$BNc$($P!"6u4V$N �$B$OC1O"7k$G$"$k�(B
(�$B>c32J*$,2?$b$J$$$N$G!"JD6J@~$O$R$C$+$+$j$h$&$,$J$$�(B)�$B!#�(B
2�$Bl9g$O!"�(B
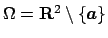 �$B$N$h$&$J7j$,$"$$$F$$$k$b$N$O�(B
�$BC1O"7k$G$O$J$$!#�(B
�$B$N$h$&$J7j$,$"$$$F$$$k$b$N$O�(B
�$BC1O"7k$G$O$J$$!#�(B
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.