12.1 Newton法

まずは定番の $x^2-2=0$ の解。

test-newton.py

# test-newton.py
def newton(f, df, x0, eps):
  x = x0
  for i in range(10):
    dx = f(x) / df(x)
    x = x - dx
    # print('Δx=%e, x=%g, f(x)=%e' % (dx, x, f(x)))
    if abs(dx) < eps:
      return x
  print('newton: 収束しませんでした。修正量=%e' % (dx))
  return x

def f(x):
  return x*x-2.0

def df(x):
  return 2*x

newton(f,df,2.0,1e-15)

方程式がパラメーターつき、つまり $f(x,\alpha)=0$ の形をしていることがあるので、 オプションでパラメーターが渡せると良いのかな？

SIRモデルで、$t=0$ でほぼ全人口が感受性者の場合 ( $O<I(0)\ll 1$, $S(0)\simeq 1$, $R(0)=0$)に、最終的残る感受性者数 $S =S(\infty)$ は

$$1-S+log\frac{S}{R_0}=0$$

の実数解のうち$1$でない方である。 ここで $R_0$ は基本再生産数というパラメーターである (流行する $R_0>1$ という場合を考える)。

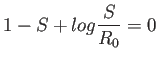
test-newton3.py

# test-newton3.py
import numpy as np
import matplotlib.pyplot as plt

def newton(f, df, x0, eps, *args):
  x = x0
  for i in range(10):
    dx = f(x, *args) / df(x, *args)
    x = x - dx
    # print('Δx=%e, x=%g, f(x)=%e' % (dx, x, f(x)))
    if abs(dx) < eps:
      return x
  print('newton: 収束しませんでした。初期値=%g, 修正量=%e' % (x0,dx))
  return x

# 解きたい方程式 f(x)=0 の f()
def I(S,R0=2.5):
  return 1.0-S+np.log(S)/R0

# f() の導関数
def dI(S,R0=2.5):
  return -1.0 + 1.0/(R0*S)

# 感染せずに残る感受性者の割合を求める
n=40
R0s=np.linspace(1.1,5.0,n+1)
left=np.empty_like(R0s)
for i in range(n+1):
  R0=R0s[i]
  if i==0:
    left[i]=newton(I,dI,0.8,1e-15,R0)
  else:
    left[i]=newton(I,dI,0.5*left[i-1],1e-15,R0)

plt.plot(R0s,1.0-left)
plt.title('基本再生産数と最終的に感染した人の割合')
plt.show()
#for i in range(n+1):
#  print(left[i])