8.1 ウォーミング・アップで Poisson 方程式

正方形領域 $\Omega=(0,1)\times(0,1)$ で

$$-\Laplacian u=f$$   in $\Omega$$$,\quad u=0$$   on $\rd\Omega$

を解く。ただし $f\equiv 1$ とする (この点は一般的なプログラムに直したい)。

差分方程式は

$$A\Vector{U}=\Vector{f},$$

ただし

$$A=I_{N_y-1}\otimes\frac{1}{h_x^2}(2I_{N_x-1}-J_{N_x-1}) +\frac{1}{h_y^2}(2I_{N_y-1}-J_{N_y-1})\otimes I_{N_x-1},$$

$$\Vector{f}=\left(f_1,\dots,f_{(N_x-1)(N_y-1)}\right)^T,\quad \Vector{U}=\left(U_1,\dots,U_{(N_x-1)(N_y-1)}\right)^T,$$

$$f_{(j-1)(N_x-1)+i}=f(x_i,y_j) 1\le i\le N_x-1 1\le j\le N_y-1 ,$$

$$U_{(j-1)(N_x-1)+i}=U_{ij} 1\le i\le N_x-1 1\le j\le N_y-1 .$$

この差分方程式の導出については， 詳しくは例えば桂田 [1] を見よ。

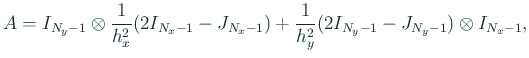MATLAB では，例えば次のようなプログラムが使える。

sparse_poisson.m

% sparse_poisson.m --- 正方形領域における Poisson 方程式 (2009/12/29)
function [x,y,u]=sparse_poisson(n)
  h=1/n;
  J=sparse(diag(ones(n-2,1),1)+diag(ones(n-2,1),-1));
  I=speye(n-1,n-1);
  A=-4*kron(I,I)+kron(J,I)+kron(I,J);
  b=-h*h*ones((n-1)*(n-1),1);
% 2次元化を少し工夫
  U=zeros(n-1,n-1);
  U(:)=A\b;
  u=zeros(n+1,n+1);
  u(2:n,2:n)=U;
  
  x=0:1/n:1;
  y=x;
% まず鳥瞰図
  subplot(1,2,1);
  colormap hsv
  mesh(x,y,u);
  colorbar
% 等高線
  right=subplot(1,2,2);
  contour(x,y,u);
  pbaspect(right,[1 1 1]);
% PostScript を出力
  disp('saving graphs');
  print -depsc2 sparsepoisson.eps

使い方は単純で，

>> sparse_poisson(100)

のようにする ($100$ は各辺を$100$等分するということ)。

図 6: MATLAB プログラム sparse_poisson.m による計算

次に掲げるのは Python 用のプログラム(試作品)である。

poisson2_v3.py

#!/opt/local/bin/python2
# -*- coding: utf-8 -*-
# poisson2_v3.py

import numpy as np
import scipy as sci
import scipy.sparse
import scipy.sparse.linalg
import matplotlib.pyplot as plot
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm

n=100
h=1.0/n
I=sci.sparse.eye(n-1,n-1)
J=sci.sparse.spdiags([np.ones(n-1),np.ones(n-1)],[1,-1],n-1,n-1)
L=-2*I+J
A=sci.sparse.kron(I,L)+sci.sparse.kron(L,I)

b=-h*h*np.ones(((n-1)*(n-1),1))
x=sci.sparse.linalg.spsolve(A,b)

u=np.zeros((n+1,n+1))
u[1:n,1:n]=x.reshape((n-1,n-1))

x=np.linspace(0.0,1.0,n+1)
y=np.linspace(0.0,1.0,n+1)
x,y=np.meshgrid(x,y)

fig=plot.figure('Poission eq')

ax1=fig.add_subplot(121, aspect='equal')
ax1.contour(x,y,u)
ax2=fig.add_subplot(122, aspect='equal', projection='3d')
surf=ax2.plot_surface(x,y,u,rstride=1,cstride=1,
                      cmap=cm.coolwarm,linewidth=0,antialiased=False)
plot.show()

poisson2_v4.py

#!/opt/local/bin/python2
# -*- coding: utf-8 -*-
# poisson2_v4.py

import numpy as np
import scipy as sci
import scipy.sparse
import scipy.sparse.linalg
import matplotlib.pyplot as plot
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm

W=2.0
H=1.0
Nx=200
Ny=100
hx=W/Nx
hy=H/Ny
Ix=sci.sparse.eye(Nx-1,Nx-1)
Iy=sci.sparse.eye(Ny-1,Ny-1)
Jx=sci.sparse.spdiags([np.ones(Nx-1),np.ones(Nx-1)],[1,-1],Nx-1,Nx-1)
Jy=sci.sparse.spdiags([np.ones(Ny-1),np.ones(Ny-1)],[1,-1],Ny-1,Ny-1)
Lx=(-2*Ix+Jx)/(hx*hx)
Ly=(-2*Iy+Jy)/(hy*hy)
A=sci.sparse.kron(Iy,Lx)+sci.sparse.kron(Ly,Ix)

b=-np.ones(((Nx-1)*(Ny-1),1))
x=sci.sparse.linalg.spsolve(A,b)

# 桂田研の2次元配列の1次元配列化は実は Fortran 流！(column-major というやつ)
# そういう意味では、これを 2 次元配列に reshape() するには
#   u=np.zeros((Nx+1,Ny+1))
#   u[1:Nx,1:Ny]=x.reshape((Nx-1,Ny-1),'F')
# とするのが自然だ。
# ところが…meshgrid()で仮定されている配列は (Ny+1,Nx+1) という形だ！
# 上の u を描画するには、u.T と転置しないといけなくなる。
# そこで Fortran 流に並んでいるものを C 流 (row-major) に reshape() する。
# これで転置をしたことになる。
u=np.zeros((Ny+1,Nx+1))
u[1:Ny,1:Nx]=x.reshape((Ny-1,Nx-1))

x=np.linspace(0.0,W,Nx+1)
y=np.linspace(0.0,H,Ny+1)
x,y=np.meshgrid(x,y)

fig=plot.figure('Poission eq')

ax1=fig.add_subplot(121, aspect='equal')
ax1.contour(x,y,u)
ax2=fig.add_subplot(122, aspect='equal', projection='3d')
surf=ax2.plot_surface(x,y,u,rstride=1,cstride=1,
                      cmap=cm.coolwarm,linewidth=0,antialiased=False)
plot.show()

図 7: Pythonプログラム poisson_v2.py による計算