Next: 7 1次元熱方程式を試す Up: 6 matplotlib Previous: 6.5 1変数関数の可視化
等高線 contour(), contourf() で等高線の描画が出来る (後者は塗りつぶしをする)。
| test_contour.py |
# test_contour.py
# 2変数関数の等高線
import numpy as np
import matplotlib.pyplot as plt
# データの準備
xmin=-1; xmax=1; ymin=-1; ymax=1; nx=100; ny=100
xs=np.linspace(xmin,xmax,nx+1)
ys=np.linspace(ymin,ymax,ny+1)
x,y=np.meshgrid(xs,ys)
z=np.sqrt(x*x+y*y+0.1)
# 等高線描画
level=np.linspace(0.0,2.0,30+1) # リストでも可
fig,ax=plt.subplots()
ax.contour(x,y,z,levels=level,cmap='jet')
# plt.xlim([xmin,xmax]); plt.ylim([ymin,ymax])
ax.set_aspect('equal') # 縦/横 を指定
plt.show()
|
| test_graph.py |
# 2変数関数のグラフの鳥瞰図 import numpy as np import matplotlib.pyplot as plt # データを準備 xmin=-1; xmax=1; ymin=-1; ymax=1; nx=100; ny=100 xs=np.linspace(xmin,xmax,nx+1) ys=np.linspace(ymin,ymax,ny+1) x,y=np.meshgrid(xs,ys) z=np.sqrt(x*x+y*y+0.1) # グラフを描画 fig=plt.figure(figsize=(6,6),facecolor='w') ax = fig.add_subplot(111, projection='3d') # 111, はなくても良い mysurface=ax.plot_surface(x,y,z,cmap='jet') # cmap='jet' とか color='b' plt.show() |
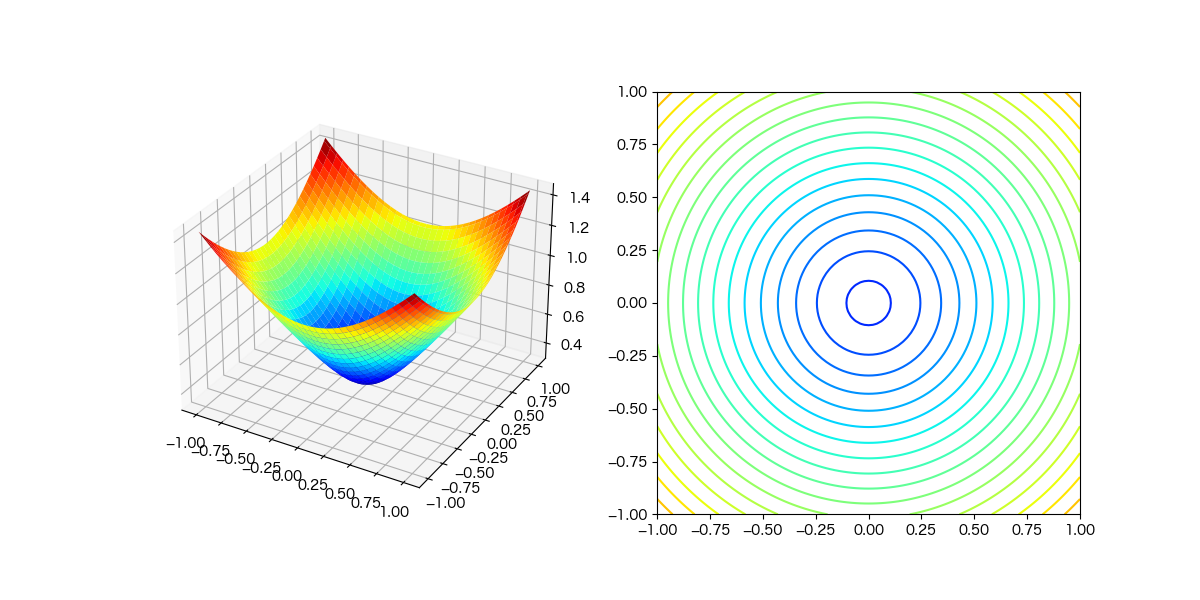
| test_graph_contour.py |
# 2変数関数のグラフと等高線
import numpy as np
import matplotlib.pyplot as plt
# データ準備
xmin=-1; xmax=1; ymin=-1; ymax=1; nx=100; ny=100
xs=np.linspace(xmin,xmax,nx+1)
ys=np.linspace(ymin,ymax,ny+1)
x,y=np.meshgrid(xs,ys)
z=np.sqrt(x*x+y*y+0.1)
# グラフ
fig=plt.figure(figsize=(12,6),facecolor='w')
ax1 = fig.add_subplot(121, projection="3d") # 1行2列の1番目 --- 左
mysurface=ax1.plot_surface(x,y,z,cmap='jet')
# 等高線
ax2 = fig.add_subplot(122) # 1行2列の2番目 --- 右
level=np.linspace(0.0,2.0,30+1)
ax2.contour(x,y,z,levels=level,cmap='jet') # plt.contour() でも表示できる
ax2.set_aspect('equal')
#ax2.set_xlim([xmin,xmax]) # plt.xlim() でも出来る
#ax2.set_ylim([ymin,ymax]) # plt.ylim() でも出来る
plt.show()
|
quiver() を用いるとベクトル場を描くことが出来る (MATLAB がそうなんだな。quiver には「震える」という意味があって、 それしか知らなかったので変な名前だと思ったけれど、 「箙(えびら)の矢; 矢筒」という意味があるそうな…えびらなんて知らない)。
| test_quiver.py |
# test_quiver.py
# 2変数関数のグラフの鳥瞰図
import numpy as np
import matplotlib.pyplot as plt
R0=2.5
# データを準備
smin=0; smax=1; imin=0; imax=1; ns=15; ni=15
xs=np.linspace(smin,smax,ns+1)
ys=np.linspace(imin,imax,ni+1)
s,i=np.meshgrid(xs,ys)
v1=-R0*s*i
v2=R0*s*i-i
# グラフを描画
# plt.quiver() とも出来るけれど
fig,ax = plt.subplots()
ax.set_aspect('equal')
ax.quiver(s,i,v1,v2)
#ax.streamplot(s,i,v1,v2)
ax.grid()
plt.show()
|
quiverkey() で矢印の説明 (凡例というのかな) が出来る。
q=ax.quiver(s,i,v1,v2)
ax.quiverkey(q, X=0.3, Y=1.05, U=1,
label='Quiver key, length = 1', labelpos='E')
|
矢印はたくさん描くと見にくくなるので、上のプログラムでは ns, ni を 15 としたが、何か他の目的で幅の狭い格子点での値を計算する場合は、 スライスを使って (s[::5,::5] のように) “飛ばして” 値を拾うと良い。
また矢印の長さを調節するには ,scale=比率 が使える。
ns = 100; ni = 100(中略) q=ax.quiver(s[::5,::5],i[::5,::5],v1[::5,::5],v2[::5,::5],scale=10) |
ベクトル場の流線
| test_streamplot.py |
# test_quiver.py
# 2変数関数のグラフの鳥瞰図
import numpy as np
import matplotlib.pyplot as plt
R0=2.5
# データを準備
smin=0; smax=1; imin=0; imax=1; ns=15; ni=15
xs=np.linspace(smin,smax,ns+1)
ys=np.linspace(imin,imax,ni+1)
s,i=np.meshgrid(xs,ys)
v1=-R0*s*i
v2=R0*s*i-i
# グラフを描画
# plt.quiver() とも出来るけれど
fig,ax = plt.subplots()
ax.set_aspect('equal')
#ax.quiver(s,i,v1,v2)
ax.streamplot(s,i,v1,v2)
ax.grid()
plt.show()
|