B..2.2 単振動の方程式

単振動の方程式の初期値問題

を解いてみよう。これは2階方程式であるが、既に説明した方法によって

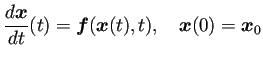$$\frac{\D\bm{x}}{\D t}(t)=\bm{f}(\bm{x}(t),t),\quad \bm{x}(0)=\bm{x}_0$$ (B.6)

という1階正規形の微分方程式の初期値問題に変換される。 ただし

$$v(t):=x'(t),\quad x_1(t):=x(t),\quad x_2(t):=v(t),\quad \bm{x}(... ...2 x_1 \end{pmatrix},\quad \bm{x}_0:=\begin{pmatrix} x_0\\ v_0 \end{pmatrix}$$

である。

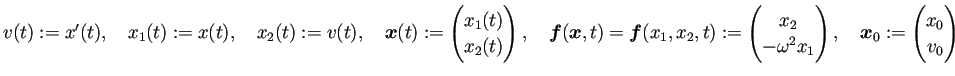
これは2次元の微分方程式である点が、Malthusモデルとは違っていて、 計算の仕方、可視化の仕方に少し違いがある。それを実例で示そう。

このやり方を応用して、Lotka-Volterra 方程式を解くことも出来る。

shm1.py -- scipy.integrate odeint() で解く

# shm1.py --- simple harmonic motion
#
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# X=[X[0],X[1]]=(x,x'), f(X)=(X[1],-ω^2 X[0]]
def shm(x, t, omega2):
    return [x[1], -omega2 * x[0]]

omega = 1; omega2 = omega * omega
t0=0; T=20; n=100; t=np.linspace(t0, T, n+1)
x0=1; v0=0; X0=[x0,v0]
X=odeint(shm, X0, t, args=(omega2,))

plt.title("単振動: x''=-ω^2 x, ω="+str(omega)+", (x(0),x'(0))=("+str(x0)+','+str(v0)+')')
plt.plot(t,X[:,0],'b', label='x')
plt.plot(t,X[:,1],'g', label='v')
plt.legend(loc='best')
plt.xlabel('t')
plt.ylabel('x and dx/dt')
plt.grid()
plt.show()

図 12: 単振動: $x(t)$ と $v(t)=dx/dt(t)$ の時間変化

$X_1(t)=x(t)$ と $X_2(t)=x'(t)$ のグラフを描いたわけであるが、 解曲線 (ベクトル値関数 $\bm{X}(t)=(X_1(t),X_2(t))$ のグラフ) は、 $\mathbb{R}^3$ 内の曲線である。 それを描くにはどうすればよいかは後述する。

(このプログラムでは、タイトルに日本語を使っている。 現時点では、自分で設定しないと日本語が表示されずに文字化けして、 警告が表示される。設定法については、 付録H.3 を見よ。 設定が面倒な場合は、プログラム内の “単振動” を削ればよい。)

初期値を色々変えた複数の解を求め、それらの解軌道 (解の像) を描いてみよう。

shm2.py

# shm2.py --- simple harmonic motion
#
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# X=[X[0],X[1]]=(x,x'), f(X)=(X[1],-ω^2 X[0]]
def shm(x, t, omega2):
    return [x[1], -omega2 * x[0]]

omega = 1; omega2 = omega * omega
t0=0; T=20; n=100; t=np.linspace(t0, T, n+1)
for i in range(0,30):
  x0=0.1*i; v0=0; X0=[x0,v0]
  X=odeint(shm, X0, t, args=(omega2,))
  plt.plot(X[:,0],X[:,1])

plt.title("単振動: x''=-ω^2 x, ω="+str(omega)+"の相図")
plt.legend(loc='best')
plt.xlim(-2,2)
plt.ylim(-2,2)
plt.xlabel('x')
plt.ylabel('dx/dt')
plt.grid()
plt.show()

図 13: 単振動: $x(t)$ と $v(t)=dx/dt(t)$ の相図

解のグラフと解軌道の両方を描くプログラム例も紹介しておく。 こちらは (半分気分転換で) scipy.integrate の solve_ivp() を使う。

まず、$X_1$, $X_2=v$ のグラフと、解軌道を描く。

shm_graph_orbit.py

# shm_graph_orbit.py --- simple harmonic motion
# coding: utf-8
#
import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt

# x=(x1, x2), f(x)=(x2,-ω^2 x_1)
def shm(t, x, omega):
    return [x[1], -omega*omega*x[0]]

omega=2.5
x0=[1.0,0.0]
Tmax=20.0
sol=solve_ivp(shm, [0.0, Tmax], x0, args=(omega,),
              dense_output=True, rtol=1e-10,atol=1e-10)
n=2000
t=np.linspace(0.0, Tmax, n+1)
x = sol.sol(t)

plt.figure(figsize=(15,5))

plt.subplot(121)
plt.plot(t,x.T)
plt.xlabel('t')
plt.legend(['x', 'v=dx/dt'], shadow=True)
plt.title('simple harmonic motion (t-x,v)')

plt.subplot(122)
plt.xlim(-1.0,1.0)
plt.plot(x[0], x[1], "-")
plt.xlabel("x")
plt.ylabel("v")
plt.title("orbit in xv-plane")

plt.show()

図 14: 単振動の解のグラフと解軌道

いわゆる解曲線というのは $t\mapsto (x(t),v(t))$ のグラフのことだから、 3次元空間の中の曲線である。これも描いてみよう。

shm_graph_orbit_v2.py

# shm_graph_orbit_v2.py --- simple harmonic motion
# coding: utf-8
#
import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt

# x=(x1, x2), f(x)=(x2,-ω^2 x_1)
def shm(t, x, omega):
    return [x[1], -omega*omega*x[0]]

omega=2.5
x0=[1.0,0.0]
Tmax=20.0
sol=solve_ivp(shm, [0.0, Tmax], x0, args=(omega,),
              dense_output=True, rtol=1e-10,atol=1e-10)
n=2000
t=np.linspace(0.0, Tmax, n+1)
x = sol.sol(t)

fig=plt.figure(figsize=(15,5))

plt.subplot(131)
plt.plot(t,x.T)
plt.xlabel('t')
plt.ylabel('x,v')
plt.legend(['x', 'v=dx/dt'], shadow=True)
plt.title('simple harmonic motion (t-x,v), ω='+str(omega))

plt.subplot(132)
plt.xlim(-1.0,1.0)
plt.plot(x[0], x[1], "-")
plt.xlabel("x")
plt.ylabel("v")
plt.title("orbit in xv-plane")

# SIR空間での軌道
# 3DAxesを追加
ax = fig.add_subplot(133, projection='3d')
# 軸ラベルを設定
ax.set_xlabel("$t$")
ax.set_ylabel("$x$")
ax.set_zlabel("$v$")
#曲線を描画
ax.plot(t, x[0], x[1])
plt.title("solution curve")

plt.show()

図 15: 単振動の解のグラフと解軌道