
Next: A. 数値計算するための情報
Up: 常微分方程式の初期値問題の数値解法
Previous: 9 参考書
急速に 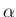 に収束する列
に収束する列
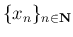 があるとき、
があるとき、
で定義される誤差の大きさについて、十分先の番号 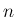 に対しては
に対しては
が成り立つので、
よって
を 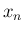 の誤差の大きさ
の誤差の大きさ 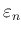 の見積りとすることが出来る。
の見積りとすることが出来る。
急速に収束しない列の場合はどうか?例えば 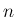 を分割数とした時の差分
法の解
を分割数とした時の差分
法の解 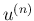 などでは、この仮定が成り立たないと思われる。
そういう場合は例えば
などでは、この仮定が成り立たないと思われる。
そういう場合は例えば
とすることによって、同じテクニックが使える。つまり例えば 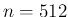 のと
きの近似解と
のと
きの近似解と 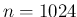 の時の近似解の差の大きさを、
の時の近似解の差の大きさを、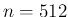 の時の近似解
の誤差の大きさの見積りとすることが出来る。
の時の近似解
の誤差の大きさの見積りとすることが出来る。


Next: A. 数値計算するための情報
Up: 常微分方程式の初期値問題の数値解法
Previous: 9 参考書
桂田 祐史
2015-05-30
![]() に収束する列
に収束する列
![]() があるとき、
があるとき、
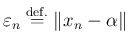
![]() を分割数とした時の差分
法の解
を分割数とした時の差分
法の解 ![]() などでは、この仮定が成り立たないと思われる。
そういう場合は例えば
などでは、この仮定が成り立たないと思われる。
そういう場合は例えば