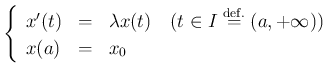
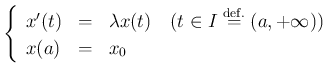
について適用してみる。この解は
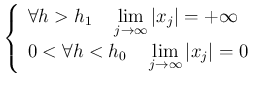
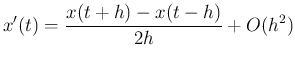
を用いて作った公式
のことを指す。 これは任意の
中心差分近似に基づく中点公式
![]() で
で
![]() ,
, ![]() を解く(
を解く(
![]() )。左側は
)。左側は
![]() としたもの、右側は
としたもの、右側は
![]() とした
もの。
とした
もの。
![\includegraphics[width=7cm]{figure/test-4.35.eps}](img275.gif)
![\includegraphics[width=7cm]{figure/test-4.35-by-midpoint2.eps}](img276.gif)
のように書ける。 ここで
なる
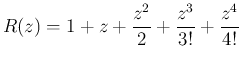 .
この
.
この
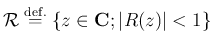
を絶対安定領域といい、
がなりたつ。 絶対安定領域が左半平面
![\includegraphics[width=6cm]{figure/myrunge.eps}](img287.gif)
![\includegraphics[width=8cm]{figure/Absolute-Stable-Region-for-Runge.eps}](img288.gif)
なお、レベル ![]() の等高線が負軸と交わる点の座標は(巾根で書けはするの
だけれど...)、
の等高線が負軸と交わる点の座標は(巾根で書けはするの
だけれど...)、
なお、後述の硬い方程式の項を参照せよ。
に対して特性方程式を
で定義し、その根を
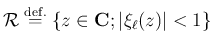
とおくと