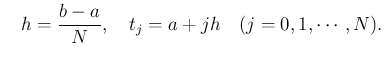

Next: 2.2.1 前進 Euler 法
Up: 2 常微分方程式の初期値問題の復習
Previous: 2.1 数学理論
(コンピューター・プログラミングの演習で、
必ずと言って良いほど出会うポピュラーな数値解法を復習しよう。)
![$ I=[a,b]$](img32.gif) とする。
とする。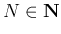 に対し、
に対し、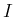 を
を 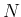 個の小区間に分ける:
個の小区間に分ける:
このとき、
各 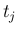 における
における 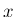 の値
の値 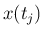 の近似値
の近似値 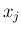 を求めることを
考える方法を離散変数法 (discrete variable
method) と呼ぶ。
を求めることを
考える方法を離散変数法 (discrete variable
method) と呼ぶ。
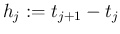 (
(
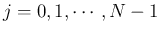 ) を刻み幅と呼ぶ。
) を刻み幅と呼ぶ。
区間の分割の仕方としては、例えば
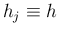
i.e.
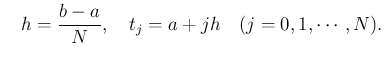
のように等分割することが多い。
以下この小節ではそれを仮定して説明するが、
可変刻み幅に一般化することは容易である。
Subsections


Next: 2.2.1 前進 Euler 法
Up: 2 常微分方程式の初期値問題の復習
Previous: 2.1 数学理論
桂田 祐史
2015-05-30
![]() とする。
とする。![]() に対し、
に対し、![]() を
を ![]() 個の小区間に分ける:
個の小区間に分ける: