

Next: 5.1 PC (予測子修正子法)
Up: 常微分方程式の初期値問題の数値解法
Previous: 4.7.4.5 testrkf1 の実行結果の分析
(この節は工事中というか、大工事が必要と考えて欲しい。)
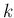 段法の公式のところで、
段法の公式のところで、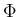 が線形の場合、
すなわち
が線形の場合、
すなわち
を線形多段法 (linear multistep method) と言う。ただし
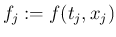 .
.
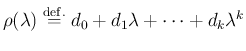 の根
の根
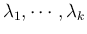 について
について
という条件が安定条件である。
多段法には以下の特徴がある。
-
- (i).
- 出発にあたって、未知の値
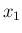 ,
, 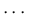 ,
, 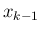 を何らの方法で求
めねばならない。
を何らの方法で求
めねばならない。
- (ii).
- 計算の途中で stepsize
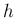 を変更するのが難しい。
を変更するのが難しい。
- (iii).
- ステップあたりの
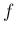 の計算回数が少ないままで、高次の公式が作れる。
の計算回数が少ないままで、高次の公式が作れる。
- (iv).
- 安定性に注意が必要。
Subsections


Next: 5.1 PC (予測子修正子法)
Up: 常微分方程式の初期値問題の数値解法
Previous: 4.7.4.5 testrkf1 の実行結果の分析
桂田 祐史
2015-05-30
![]() 段法の公式のところで、
段法の公式のところで、![]() が線形の場合、
すなわち
が線形の場合、
すなわち
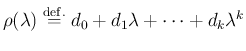 の根
の根
![]() について
について