(この節の内容は全面的に杉原・室田 [23] のつまみ食いである。)
平野法は Newton 法を少し修正したものであるが、
大域的収束性を保証できるという大きな長所がある。1960 年代後半に
- 平野 菅保, 代数方程式の解法および誤差, 第8回プログラミングシンポジウム
報告集, 情報処理学会, 1967.
- B. Dejon and K. Nickel, A never failing fast convergent root-finding
algorithm, Constructive Aspects of the Fundamental Theorems of
Algebra (B. Dejon and P. Henrici, eds.), John Wiley, New York, 1969, pp. 1-35.
によって独立に提案された算法である。
アルゴリズムの解説と収束を保証する定理については、
室田 一雄, 平野の変形 Newton 法の大域的収束性, 情報処理学会論文誌,
Vol.21 (1980), pp. 469-474.
で初めて証明された。
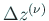 は次のように考えて決める。
は次のように考えて決める。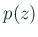 を
を 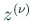 の回
りで
の回
りで
|
(A.1) |
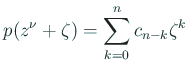 |
と展開する。もちろん
特に
通常の Newton 方では、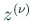 が根に十分近いことを前提にして、
(A.1) の右辺から
が根に十分近いことを前提にして、
(A.1) の右辺から 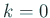 と
と 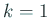 に対応する
項だけを取り出して、
に対応する
項だけを取り出して、
|
(A.2) |
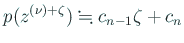 |
と近似して、これを 0 にする値
を修正量としている。
平野法では、
という 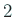 項近似を考え、これから定まる
項近似を考え、これから定まる
を修正量の候補とし、それらの中で絶対値が最小のもの (これを 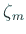 と
書く) を修正量に採用する。
と
書く) を修正量に採用する。
証明.
杉原・室田 [
23] を見よ。


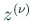 が根
が根 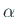 の十分良い近似値ならば
の十分良い近似値ならば 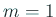 となる (すなわ
ち Newton 法と一致)。さらに
となる (すなわ
ち Newton 法と一致)。さらに 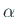 が単根であることを仮定すると、
補題の条件が成り立つ。
が単根であることを仮定すると、
補題の条件が成り立つ。
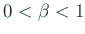 ,
, 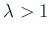 は減速の仕方を決めるパラメーターである。
例えば
は減速の仕方を決めるパラメーターである。
例えば 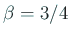 ,
, 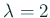 とする。
とする。
平野法の第 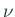 段の修正量の決定 段の修正量の決定 |
- (1)
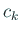 ( (
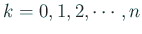 ) を組み立て除法で計算する。 ) を組み立て除法で計算する。
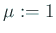 とおく。 とおく。
- (2)
-
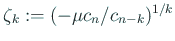 ( (
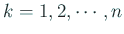 ) とおく。 ) とおく。
- (3)
-
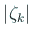 が最小である が最小である 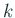 ( (
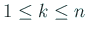 ) を ) を 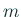 とおく。 とおく。
- (4)
-
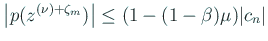 ならば、 ならば、
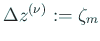 として第 として第 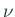 段を終了し、
そうでなければ 段を終了し、
そうでなければ
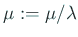 として、(2) に戻る。 として、(2) に戻る。
|
(2) における 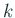 乗根の分枝は、
乗根の分枝は、
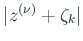 が最も小さくなるなものを選ぶ。
具体的には
が最も小さくなるなものを選ぶ。
具体的には 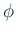 ,
,
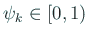 を
を
で定めて、
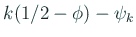 に最も近い整数
に最も近い整数 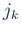 を求め、
を求め、
|
(A.3) |
![$\displaystyle \zeta_k:= \left\vert \mu\frac{c_n}{c_{n-k}} \right\vert^{1/k} \exp \left[ \frac{2\pi i(\psi_k+j_k)}{k} \right]$](img342.gif) |
とする。
証明.
元々は室田 [
23] による。杉原・室田 [
23] 第5章を見
よ。


桂田 祐史
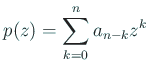
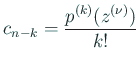
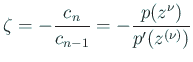
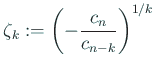

![]() が根
が根 ![]() の十分良い近似値ならば
の十分良い近似値ならば ![]() となる (すなわ
ち Newton 法と一致)。さらに
となる (すなわ
ち Newton 法と一致)。さらに ![]() が単根であることを仮定すると、
補題の条件が成り立つ。
が単根であることを仮定すると、
補題の条件が成り立つ。
![]() ,
, ![]() は減速の仕方を決めるパラメーターである。
例えば
は減速の仕方を決めるパラメーターである。
例えば ![]() ,
, ![]() とする。
とする。
![]() 乗根の分枝は、
乗根の分枝は、
![]() が最も小さくなるなものを選ぶ。
具体的には
が最も小さくなるなものを選ぶ。
具体的には ![]() ,
,
![]() を
を
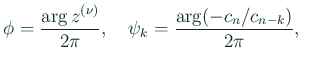
![$\displaystyle \zeta_k:= \left\vert \mu\frac{c_n}{c_{n-k}} \right\vert^{1/k} \exp \left[ \frac{2\pi i(\psi_k+j_k)}{k} \right]$](img342.gif)
![\begin{jtheorem}[室田 1980 - 平野法の大域的収束性]
任意の初�...
...��に $\{z^{(\nu)}\}$ は $p(z)$ のある根に収束する。
\end{jtheorem}](img343.gif)