C..3 2次元熱方程式陽解法

2次元の正方形領域 $\Omega= (0,1)\times(0,1)$ における熱方程式の初期値境界値問題

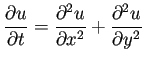		$\displaystyle \frac{\rd u}{\rd t}=\frac{\rd^2 u}{\rd x^2}+\frac{\rd^2 u}{\rd y^2}$ ( $(x,y)\in\Omega$ , )
		$\displaystyle u(x,y,t)=0$ ( $(x,y)\in\rd\Omega$ , )
		$\displaystyle u(x,y,0)=u_0(x,y)$ ( $(x,y)\in\overline{\Omega}$ )

アルゴリズムは標準的なもので、どこでも見られるが、例えば「熱方程式に対する差分法 I」に説明がある。

まず可視化を gnuplot で行うバージョンを示す。

# heat2d_e_gnuplot.jl --- 空間2次元熱方程式の初期値境界値問題 (Dirichlet,Euler) #= using Printf # @printf using LinearAlgebra # norm() include("heat2d_e_gnuplot.jl") heat2d_e_gnuplot(0.05,0.0005,100,50,0.5) 80.647537 seconds (18.70 M allocations: 442.070 MiB, 0.12% gc time) =# # 初期値 function u0(x,y) sin(5 * pi * x) * sin(3 * pi * y) end # gnuplot で u を描画 function drawgraph(t, x, y, u, gp) m,n=size(u) @printf(gp, "splot '-' with lines title \"t=%.3f\"\n", t) for i=1:m for j=1:n @printf(gp, "%f %f %f\n", x[i], y[j], u[i,j]) end @printf(gp, "\n") end @printf(gp, "e\n") flush(gp) end function heat2d_e_gnuplot(tMax=0.05, dt=0.0005, Nx=100, Ny=50, lambda=0.5) a = 0.0; b = 2.0; c = 0.0; d = 1.0 hx = (b - a) / Nx; hy = (d - c) / Ny; hx2 = hx * hx; hy2 = hy * hy tau = lambda * (hx2 * hy2) / (hx2 + hy2) lambdax = tau / hx2; lambday = tau / hy2 nMax = Int(ceil(tMax / tau)) nskip = max(Int(round(dt / tau)),1) # println("tMax=$tMax, Δt=$dt, Nx=$Nx, Ny=$Ny, λ=$lambda") println("hx=$hx, hy=$hy, tau=$tau") println("減衰率=e^{-2π^2 τ}=$(exp(-2*pi*pi*tau))") println("lambda=$lambda, lambdax+lambday=$(lambdax+lambday)") println("nskip=$nskip") # メモリー確保 x = range(a, b, length = Nx+1) y = range(c, d, length = Ny+1) u = u0.(x*ones(Ny+1)', ones(Nx+1)*y') newu=zeros(size(u)) # gnuplot の起動 println("gnuplot") p=open(pipeline(`gnuplot --persist`; stderr=Pipe()), "r+") println(p.in, "set xlabel \"x\"") println(p.in, "set ylabel \"y\"") println(p.in, "set zlabel \"u\"") println(p.in, "set title \"2D heat equation u_t=u_{xx}+u_{yy}\" at screen 0.4,0.95"); println(p.in, "set xrange [a:b]") println(p.in, "set yrange [c:d]") println(p.in, "set zrange [-1.0:1.0]") println(p.in, "set hidden3d") println(p.in, "set contour") # 初期値 t=0.0 drawgraph(t,x,y,u,p.in) @printf("||u(・,%g)||=%g\n", t, norm(u)) sleep(3) # 時間発展 for n=1:nMax t=n*tau newu[2:end-1,2:end-1]=((1.0-2.0*lambda)*u[2:end-1,2:end-1] + lambdax*(u[1:end-2,2:end-1]+u[3:end,2:end-1]) + lambday*(u[2:end-1,1:end-2]+u[2:end-1,3:end])) u=copy(newu) @printf("||u(・,%g)||=%g\n", t, norm(u)) if n % nskip == 0 drawgraph(t,x,y,u,p.in) end end close(p) end

ターミナルで

$ curl -O http://nalab.mind.meiji.ac.jp/~mk/misc/20191229/heat2d_e_gnuplot.jl
$ julia
julia> using Printf
julia> using LinearAlgebra
julia> include("heat2d_e_gnuplot.jl")
julia> heat2d_e_gnuplot()

差分方程式を

    newu[2:end-1,2:end-1]=((1.0-2.0*lambda)*u[2:end-1,2:end-1]
      + lambdax*(u[1:end-2,2:end-1]+u[3:end,2:end-1])
      + lambday*(u[2:end-1,1:end-2]+u[2:end-1,3:end]))
    u=copy(newu)

と書いているが、

    for i=2:Nx
      for j=2:Ny
        newu[i,j] = ((1.0-2.0*lambda) * u[i,j]
        + lambdax * (u[i+1,j]+u[i-1,j]) + lambday * (u[i,j+1]+u[i,j-1]))
      end
    end
    for i=1:Nx+1
      for j=1:Ny+1
        u[i,j]=newu[i,j]
      end
    end

と書いても、あまり変わらないようだ (この辺は自信がない)。

次に Plots を利用したバージョン。

ターミナルで

$ curl -O http://nalab.mind.meiji.ac.jp/~mk/misc/20200101/heat2d_e_plots.jl
$ julia
julia> using Printf
julia> using Plots
julia> gr()
julia> using LinearAlgebra
julia> include("heat2d_e_plots.jl")
julia> heat2d_e_plots()

plot() に渡すとき、 u を転置した u' を渡していることに注意 (' は Hermite 共役を意味するので、 transpose(u) とするのが本当かもしれない)。転置するのが嫌ならば、初期値の設定を

  u=u0.(ones(Ny+1)*x',y*ones(Nx+1)')

また差分方程式を

  newu[2:end-1,2:end-1]=((1.0-2.0*lambda)*ut[2:end-1,2:end-1]
      + lambdax*(ut[2:end-1,1:end-2]+ut[2:end-1,3:end])
      + lambday*(ut[1:end-2,2:end-1]+ut[3:end,2:end-1]))
  u=copy(newu)

とするという手もある (heat2d_e_plots_v2.jl というプログラムも用意してある)。

桂田祐史

C..3 2次元熱方程式 陽解法

C..3 2次元熱方程式陽解法