Next: E..3 Euler法の “意義” Up: E. 公式の選択 Previous: E..1 はじめに
以下、古典的な Runge-Kutta 法を単に Runge-Kutat法と呼ぶ。
局所離散化誤差、全離散化誤差という言葉の定義は省略する (桂田 [3] などを見よ)。
Euler法は1次、Runge-Kutta法は4次の公式である。
これは (刻み幅を ![]() と書くことにして、滑らかな解を持つ問題に適用したとき)
と書くことにして、滑らかな解を持つ問題に適用したとき)
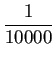 にしたければ
(精度を10進法で4桁あげたければ)、
ステップ数 (従って計算量)を、Euler 法では
にしたければ
(精度を10進法で4桁あげたければ)、
ステップ数 (従って計算量)を、Euler 法では 数値例が見たければ
次数を高くするためには、より多くの手間をかける必要があるのが普通である。
手間の目安としては、公式の段数が使われることが多い。
それは時刻を1ステップ勧めるのに、
微分方程式の右辺に現れる関数![]() を何回計算するかを表している。
Euler法は1段、Runge-Kutta法は4段である。
粗い言い方をすると、ステップ数を同じにする場合、
Runge-Kutta法はEuler法の4倍の計算量が必要ということである。
を何回計算するかを表している。
Euler法は1段、Runge-Kutta法は4段である。
粗い言い方をすると、ステップ数を同じにする場合、
Runge-Kutta法はEuler法の4倍の計算量が必要ということである。
