Next: E. 公式の選択 Up: D. 力学系についてメモ Previous: D..2 平衡点とは
![\begin{jdefinition}% latex2html id marker 1099
[平衡点の安定、不安定]
...
...��安定でないことを「不安定である」という。
\end{jdefinition}](img187.png)
|
つまり、任意の正の数 ![]() に対して、
に対して、
![]() に十分近いところから出発した任意の解は、
に十分近いところから出発した任意の解は、
![]() から距離
から距離 ![]() の範囲に止まる、ということである。
の範囲に止まる、ということである。
(私が学生で、このあたりのことを勉強したとき、「リャプノフの意味で」 というのを見て、「そうでない意味で安定というのは、例えばどういうの?」 と気になった。 でもそういうのを目にすることはなく、 最近は「リャプノフの意味で」というのは省略されるのが多くなった。 時間が経って、言葉が定着したということなのだろう。)
![\begin{jdefinition}% latex2html id marker 1106
[平衡点の漸近安定性]
(\...
...o\infty}x(t)=a
\end{displaymath}を満たすことをいう。
\end{jdefinition}](img189.png)
|
判定法として、次の定理が使われることが非常に多い。

|
「ヤコビ行列って何ですか?」
(学生が持っている教科書の索引にヤコビ行列がない…ぶつぶつ )
![]() ,
,
![]() ,
,
![]() は微分可能とするとき、
は微分可能とするとき、
![]() の
の ![]() におけるヤコビ行列とは、
におけるヤコビ行列とは、![]() 型の
行列
型の
行列
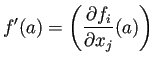
力学系
![]() においては
においては ![]() であることに注意しよう
(微分方程式の左辺は
であることに注意しよう
(微分方程式の左辺は ![]() 次元, 右辺は
次元, 右辺は ![]() 次元なので)。
ゆえに
次元なので)。
ゆえに ![]() は
は ![]() 次正方行列で、(重複度を込めて)
次正方行列で、(重複度を込めて) ![]() 個の固有値を持つ。
行列
個の固有値を持つ。
行列 ![]() の成分は実数であるが、固有値には虚数が現れることもある。
の成分は実数であるが、固有値には虚数が現れることもある。
この定理が、![]() の場合にも使えることを注意しておく。
の場合にも使えることを注意しておく。
![]() のとき、
のとき、![]() の
の ![]() におけるヤコビ行列は、
におけるヤコビ行列は、
![]() の
の ![]() における微分係数
における微分係数
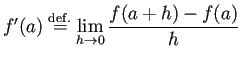 そのものである。
またその固有値は、
そのものである。
またその固有値は、![]() (これは実数) である
(一般に実数
(これは実数) である
(一般に実数 ![]() を、
を、![]() 型の実行列とみなすとき、
型の実行列とみなすとき、
![]() が
が ![]() に対して成り立つので、
に対して成り立つので、
![]() は
は ![]() の固有値で、
の固有値で、![]() が固有ベクトルである。)。
が固有ベクトルである。)。
ゆえに、定理を ![]() の場合に限定すると、
「
の場合に限定すると、
「![]() ならば
ならば ![]() は漸近安定、
は漸近安定、![]() ならば
ならば ![]() は不安定」
ということになる。
は不安定」
ということになる。