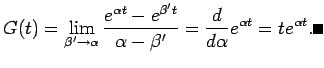4 ラプラス変換を利用する方法

ラプラス変換は、道具一式を用意するのに手間がかかるが、結局は一番見通しが良いかもしれない。ラプラス変換を袖にする数学書も多いが、学習しておく価値はあるな、と思う次第である。

$\begin{jproposition} $p$, $q$\ は実数, $f\colon[0,\infty)\to\C$\ を連続�... ...eta$\ は、2次方程式 $s^2+ps+q=0$\ の 2 根とする。 \end{jproposition}$

証明. 与えられた微分方程式をラプラス変換して、ラプラス変換の線形性を用いると

$\displaystyle L[x''(t)](s)+p L[x'(t)](s)+q L[x(t)](s)=L[f](s).$

左辺第1項と第2項に、導関数のラプラス変換の公式

$\displaystyle L\left[g^{(k)}(t)\right](s) =s^k L[g(t)](s)-s^{k-1} g(0)-s^{k-2}g'(0)-\cdots-s g^{(k-2)}(0)-g^{(k-1)}(0)$

を用いて、初期条件

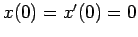
を代入すると

$\displaystyle s^2 L[x(t)](s)+p s L[x(t)](s)+q L[x(t)](s)=L[f](s).$

すなわち

$\displaystyle (s^2+p s+q)L[x(t)](s)=L[f](s)$

これを

について解くと (単に割り算するだけ)

$\displaystyle L[x(t)](s)=\frac{1}{s^2+p s+q} L[f](s).$

右辺が積の形になっていることに注目して、

$\displaystyle G(t):=L^{-1}\left[\frac{1}{s^2+ps+q}\right](t)$

とおくと、

$\displaystyle L[x(t)](s)=L[G](s) L[f](s)=L[G\ast f](s)$

となるので、逆ラプラス変換して次式を得る。

$\displaystyle x(t)=G\ast f(t).$

以下、

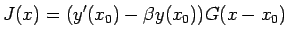
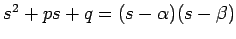
を具体的に計算する。 $s^2+p s+q=(s-\alpha)(s-\beta)$ であるから、

$\displaystyle G(t)=L^{-1}\left[\frac{1}{(s-\alpha)(s-\beta)}\right](t) =L^{-1}\... ...(t)\ast L^{-1}\left[\frac{1}{s-\beta}\right](t) =e^{\alpha t}\ast e^{\beta t}.$

これを求めるのに、もちろん畳込みの定義に従って積分計算しても良いが、次のようにラプラス変換を利用することも出来る。

(i)

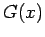$\alpha\ne \beta$ のとき、

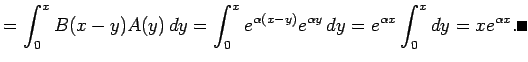$\displaystyle \frac{1}{(s-\alpha)(s-\beta)} =\frac{1}{\alpha-\beta}\left(\frac{1}{s-\alpha}-\frac{1}{s-\beta}\right)$

であるから

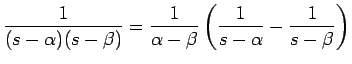
$\displaystyle G(t)=\frac{1}{\alpha-\beta} \left( L^{-1}\left[\frac{1}{s-\alpha}... ...ight](t) \right) =\frac{1}{\alpha-\beta}\left(e^{\alpha t}-e^{\beta t}\right).$

(ii)

$\alpha=\beta$ のとき、(本当はちょっと準備が必要だが)

$\displaystyle G(t)=\lim_{\beta'\to\alpha}\frac{e^{\alpha t}-e^{\beta't}}{\alpha-\beta'} =\frac{\D}{\D\alpha} e^{\alpha t}=t e^{\alpha t}. \qed$

$\qedsymbol$