Next: 3 単振動との比較 Up: 2 微分方程式の解析 Previous: 予備的考察
結果の式が簡単になるように、 適当な初期条件を課した初期値問題の解を求めよう。
![]() を
を
![]() なる定数として、
なる定数として、
| (5) | 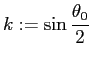 |
この初期値問題の解は
であることを示そう。
まずエネルギー保存則 (4) から
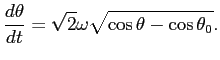
(
これは変数分離形の微分方程式である。天下りであるが、
| (7) | 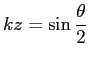 |
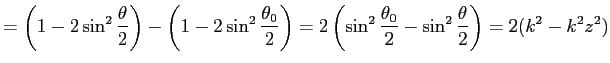 | ||
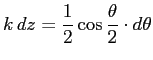
より
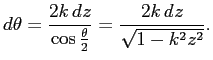
(多分、(4) を、
これから
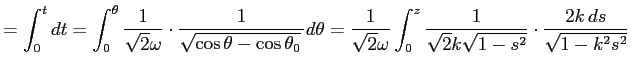 | ||
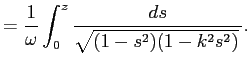 |
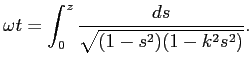
これは、Jacobi の楕円関数
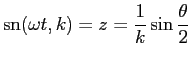
と解ける。ゆえに
| (8) |
桂田 祐史