


Next: 6.5 都合が「よくない」場合の Lanczos 法
Up: 6 Lanczos アルゴリズム
Previous: 6.3 Lanczos 原理
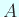 を
を 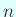 次の実対称行列で、
次の実対称行列で、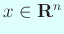 に対して、
「都合よく」
に対して、
「都合よく」
が成り立つと仮定する。前節の定理から、
をみたす実直交行列
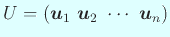 が存在する。
これから
が存在する。
これから
という条件が導かれる。
また
|
(6) |
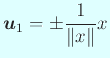 |
である。
実は
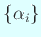 ,
,
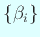 ,
,
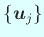 は
この条件 (5), (6) だけで定めることができる。
は
この条件 (5), (6) だけで定めることができる。
最初の式と
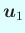 との内積を取ると
との内積を取ると
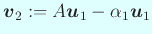 とおくと、
とおくと、
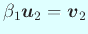 であるから、
であるから、
ゆえに
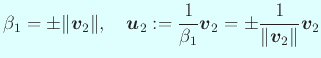
(複号同順)
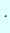
(5) の第2式と
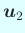 との内積を取ると、
との内積を取ると、
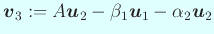 とおくと、
とおくと、
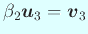 であるから、
であるから、
ゆえに
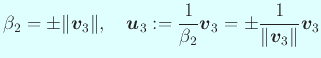
(複号同順)
以下同様にして...



Next: 6.5 都合が「よくない」場合の Lanczos 法
Up: 6 Lanczos アルゴリズム
Previous: 6.3 Lanczos 原理
桂田 祐史
2015-12-22
![]() を
を ![]() 次の実対称行列で、
次の実対称行列で、![]() に対して、
「都合よく」
に対して、
「都合よく」
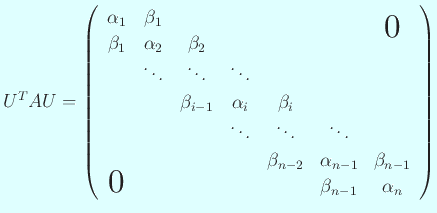
![]() との内積を取ると
との内積を取ると
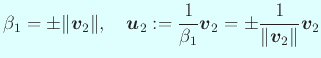 (複号同順)
(複号同順)![]() との内積を取ると、
との内積を取ると、
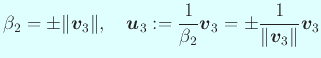 (複号同順)
(複号同順)