Next: C. Windows 環境での利用 Up: B. 実例集 Previous: B..1 例: 差分法で解いた1次元熱伝導方程式の初期値境界値問題の解の可視化
(有限要素法を出したので、差分法もやっておくべきか、 どうして気づかなかったのか?)
正方形領域
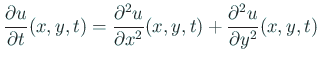 ( (
|
||
ここで ![]() は
は ![]() の境界 ((正方形の4つの辺の合併)、
の境界 ((正方形の4つの辺の合併)、
![]() は時刻
は時刻 ![]() での初期温度分布である。
での初期温度分布である。
時間発展する系なので、
各時刻 ![]() での差分解
での差分解
![]() のグラフの鳥瞰図を描くことにする。
のグラフの鳥瞰図を描くことにする。
プログラムは https://m-katsurada.sakura.ne.jp/misc/20191229/heat2d-gnuplot.cに置いておく。
| Mac のターミナルの場合: プログラムの入手、コンパイル、実行 |
curl -O https://m-katsurada.sakura.ne.jp/misc/20191229/heat2d-gnuplot.c cc heat2d-gnuplot.c ./a.out(Xcode の cc, GNU の gcc で動作確認済み) |
/*
* heat2d-gnuplot.c --- 2次元領域の熱伝導方程式
* u_t=u_{xx}+u_{yy}, 同次Dirichlet境界条件
*/
#include <stdio.h>
#include <math.h> // rint()
#include <stdlib.h> // malloc()
#include <unistd.h> // sleep()
typedef double *vector;
typedef vector *matrix;
matrix newmatrix(int m, int n)
{
int i;
vector ap;
matrix a;
if ((a = malloc(m * sizeof(vector))) == NULL)
return NULL;
if ((ap = malloc(m * n * sizeof(double))) == NULL) {
free(a);
return NULL;
}
for (i = 0; i < m; i++)
a[i] = ap + (i * n);
return a;
}
// 初期条件
double u0(double x, double y)
{
return x * (1 - x) * y * (1 - y);
}
int main(void)
{
int nx, ny, i, j, n, nMax, nskip;
double Tmax, tau, hx, hy, t, lambdax, lambday, lambda, c, dt, ztop;
double *x, *y;
matrix u, newu;
FILE *gp;
Tmax = 0.5;
dt = 0.001; // 描画間隔
// 分割
nx = 50; ny = 50;
hx = 1.0 / nx; hy = 1.0 / ny;
tau = 0.25 * (hx*hx*hy*hy)/(hx*hx+hy*hy); // λ=0.25
nskip = rint(dt / tau); if (nskip <= 0) nskip = 1;
lambdax = tau / (hx * hx);
lambday = tau / (hy * hy);
c = 1 - 2.0 * (lambdax + lambday);
nMax = Tmax / tau;
printf("hx=%g, hy=%g, tau=%g, nskip=%d\n", hx, hy, tau, nskip);
// メモリー確保
x = malloc(sizeof(double) * (nx+1));
y = malloc(sizeof(double) * (ny+1));
u = newmatrix(nx+1,ny+1);
newu = newmatrix(nx+1,ny+1);
if (x == NULL || y == NULL || u == NULL || newu == NULL) {
fprintf(stderr, "メモリー不足です。");
exit(1);
}
// gnuplot を呼び出す
if ((gp = popen("gnuplot -persist", "w")) == NULL) {
exit(1);
}
// 次の2行の注釈を外すとアニメーション GIF ファイルを作る
// fprintf(gp, "set term gif animate\n");
// fprintf(gp, "set output \"heat2d.gif\"\n");
fprintf(gp, "set xlabel \"x\"\n");
fprintf(gp, "set ylabel \"y\"\n");
fprintf(gp, "set label \"2D heat equation\" at screen 0.4,0.95\n");
fprintf(gp, "set xrange [0:1]\n");
fprintf(gp, "set yrange [0:1]\n");
// 初期値
t = 0;
for (i = 0; i <= nx; i++)
x[i] = i * hx;
for (j = 0; j <= ny; j++)
y[j] = j * hy;
for (i = 0; i <= nx; i++)
for (j = 0; j <= ny; j++)
u[i][j] = u0(x[i], y[j]);
// 初期値を描く
ztop = pow(10.0, ceil(log10(fabs(u[nx/2][ny/2]))));
fprintf(gp, "set zrange [0:%f]\n", ztop);
fprintf(gp, "splot '-' with lines title \"t=0\"\n");
for (i = 0; i <= nx; i++) {
for (j = 0; j <= ny; j++)
fprintf(gp, "%f %f %f\n", x[i], y[j], u[i][j]);
fprintf(gp, "\n");
}
fprintf(gp, "e\n");
fflush(gp);
sleep(3);
// 時間を進める
for (n = 1; n <= nMax; n++) {
t = n * tau;
for (i = 1; i < nx; i++)
for (j = 1; j < ny; j++) {
newu[i][j] = c * u[i][j]
+ lambdax * (u[i+1][j]+u[i-1][j])
+ lambday * (u[i][j+1]+u[i][j-1]);
}
for (i = 0; i <= nx; i++)
newu[i][0] = newu[i][ny] = 0.0;
for (j = 0; j <= ny; j++)
newu[0][j] = newu[nx][j] = 0.0;
for (i = 0; i <= nx; i++)
for (j = 0; j <= ny; j++)
u[i][j] = newu[i][j];
if (n % nskip == 0) {
ztop = pow(10.0, ceil(log10(fabs(u[nx/2][ny/2]))));
fprintf(gp, "set zrange [0:%f]\n", ztop);
fprintf(gp, "splot '-' with lines title \"t=%g\"\n", t);
for (i = 0; i <= nx; i++) {
for (j = 0; j <= ny; j++)
fprintf(gp, "%f %f %f\n", x[i], y[j], u[i][j]);
fprintf(gp, "\n");
}
fprintf(gp, "e\n");
fflush(gp);
}
}
pclose(gp);
return 0;
}