Next: 参考文献 Up: Mathematica で Fourier 解析 Previous: 6 WAVEファイルの内容を FFT して加工
両端を固定した長さ ![]() の弦の変位
の弦の変位 ![]()
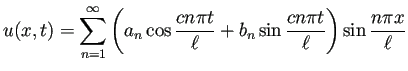
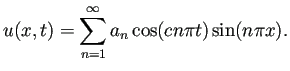
固有振動
![]() の和で表されている。
の和で表されている。
![]() の場合に固有振動がどのようなものか、見てみよう。
の場合に固有振動がどのようなものか、見てみよう。
c=1; L=1; u[n_, x_, t_] := Sin[n Pi x/L] Cos[c n Pi t/L]
Animate[Table[
Plot[{u[n, x, 0], u[n, x, t]}, {x, 0, L}, PlotRange -> {-1, 1}],
{n, 1, 3}], {t, 0, 2L/c, 0.01}]
|