Next: 12 曲線の連続的な変形 (ホモトピー) Up: 複素数と Mathematica Previous: 10 Abel の連続性定理に現れる収束範囲
以下の線積分の値を求めよ。
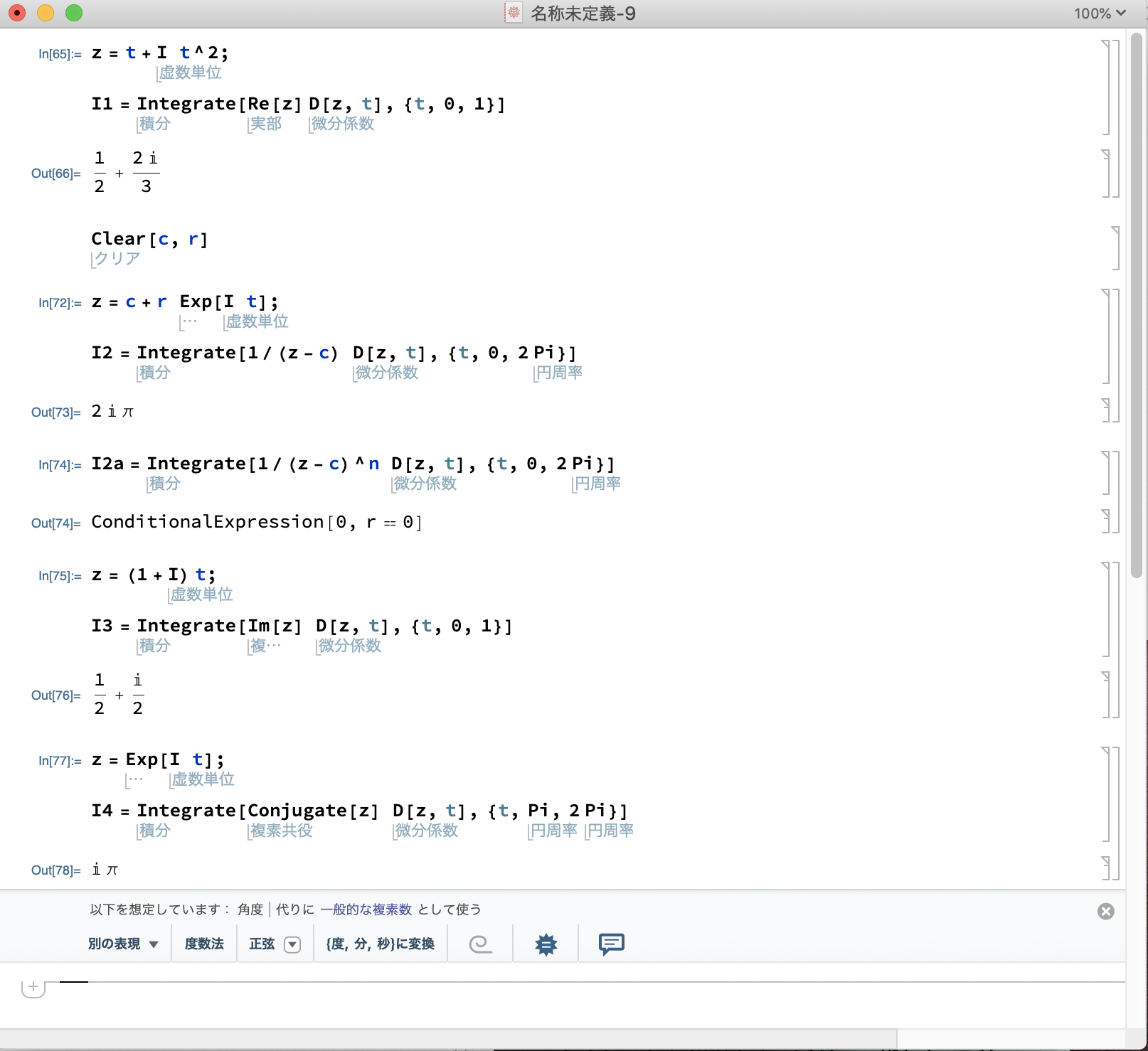
(1)
![]() (
(![]() ) とするとき
) とするとき
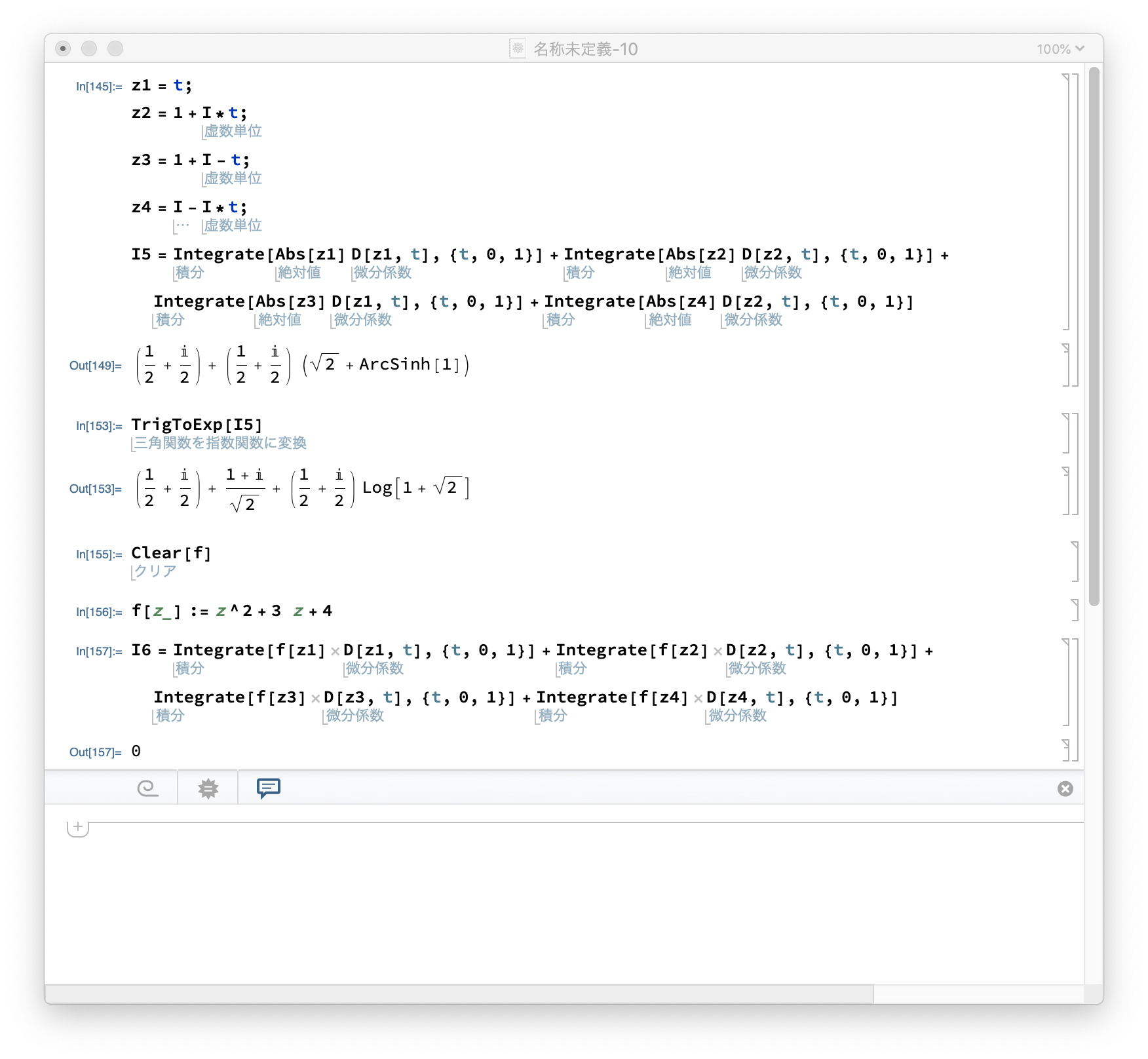
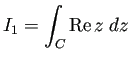 (2)
(2)
![]() ,
, ![]() ,
,
![]() ,
,
![]() (
(
![]() ) とするとき
) とするとき
 (3) 0 から
(3) 0 から ![]() に至る線分を
に至る線分を ![]() とするとき
とするとき
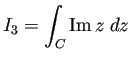 (4) 単位円
(4) 単位円 ![]() の下半分を
の下半分を ![]() から
から ![]() までたどる曲線を
までたどる曲線を ![]() とする
とき
とする
とき
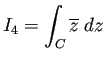 (5) 図の正方形の周を反時計回りに一周する曲線を
(5) 図の正方形の周を反時計回りに一周する曲線を ![]() とするとき
とするとき
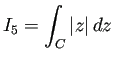 ,
,
z=t+I t^2;
I1=Integrate[Re[z]D[z,t],{t,0,1}]
z=c+r Exp[I t];
I2=Integrate[1/(z-c) D[z,t],{t,0,2Pi}]
I2a=Integrate[1/(z-c)^n D[z,t],{t,0,2Pi}]
z=(1+I)t;
I3=Integrate[Im[z] D[z,t],{t,0,1}]
z=Exp[I t];
I4=Integrate[Conjugate[z] D[z,t],{t,Pi,2Pi}]
z1=t;
z2=1+I*t;
z3=1+I-t;
z4=I-I*t;
I5=Integrate[Abs[z1]D[z1,t],{t,0,1}]+Integrate[Abs[z2]D[z2,t],{t,0,1}]
+Integrate[Abs[z3]D[z1,t],{t,0,1}]+Integrate[Abs[z4]D[z2,t],{t,0,1}]
f[z_] := z^2 + 3 z + 4
I6 = Integrate[f[z1] D[z1, t], {t, 0, 1}] +
Integrate[f[z2] D[z2, t], {t, 0, 1}] +
Integrate[f[z3] D[z3, t], {t, 0, 1}] +
Integrate[f[z4] D[z4, t], {t, 0, 1}]
|
答は (1)
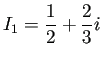 (2)
(2) ![]() のとき
のとき
![]() ,
, ![]() のとき
のとき ![]() (3)
(3)
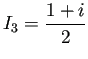 (4)
(4) ![]() (5)
(5)
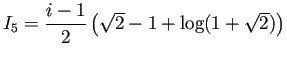 (6)
(6) ![]()
Mathematica は、(5) の
![]() を ArcSinh[1] と表示する。
TrigToExp[] を施すと
を ArcSinh[1] と表示する。
TrigToExp[] を施すと ![]() で表示してくれる。
で表示してくれる。
|
In[ ]:= TrigToExp[ArcSinh[1]]
Out[ ]= Log[1+ |